
分析 (1)先分别观察等号左右两边的特点,会发现数据是一样的只是左边是乘法计算,右边是加法计算,所以只要找到左边的变化规律,右边变为加法即可.等号左边的3个式子中,分子都是1,而分母分别是连续的整数,把分母分别与式子的序号找到对应关系,如“×”前面的负分数中分子都是1,第1个式子的分母是1,第2个式子的分母是2,第3个式子的分母是3,所以可推出第4个式子的分母是4,第5个式子的分母是5,第n个式子的分母是n,即第n个分数为:-$\frac{1}{n}$,同理可找到“×”后面的分数为$\frac{1}{n+1}$,从而得到第n个式子为:-$\frac{1}{n}$×$\frac{1}{n+1}$=-$\frac{1}{n}$+$\frac{1}{n+1}$.
(2)根据(1)中的规律把式子变形,中间部分相互抵消,只剩下首项和末项,即可算出答案.
解答 解:(1)观察各个式子可以发现:这3个式子中等号左边的规律:“×”前面的负分数中分子都是1,第1个式子的分母是1,第2个式子的分母是2,第3个式子的分母是3,所以可推出第4个式子的分母是4,第5个式子的分母是5,第n个式子的分母是n;“×”后面的分数中,分子都是1,第1个式子的分母是2,第2个式子的分母是3,第3个式子的分母是4,所以可推出第4个式子的分母是5,第5个式子的分母是6,第n个式子的分母是n+1;这3个式子中等号右边的规律是把等号左边式子中的“×”改为“+”,所以第4个等式为:-$\frac{1}{4}$×$\frac{1}{5}$=-$\frac{1}{4}$+$\frac{1}{5}$,第5个式子为:-$\frac{1}{5}$×$\frac{1}{6}$=-$\frac{1}{5}$+$\frac{1}{6}$;第n个式子为:-$\frac{1}{n}$×$\frac{1}{n+1}$=-$\frac{1}{n}$+$\frac{1}{n+1}$.
(2)由(1)中的规律“-$\frac{1}{n}$×$\frac{1}{n+1}$=-$\frac{1}{n}$+$\frac{1}{n+1}$”把式子进行变形可得:
(-1×$\frac{1}{2}$)+(-$\frac{1}{2}$×$\frac{1}{3}$)+(-$\frac{1}{3}$×$\frac{1}{4}$)+…+(-$\frac{1}{2012}$×$\frac{1}{2013}$)+(-$\frac{1}{2013}$×$\frac{1}{2014}$)
=-1+$\frac{1}{2}$-$\frac{1}{2}$+$\frac{1}{3}$-$\frac{1}{3}$+$\frac{1}{4}$+…-$\frac{1}{2012}$+$\frac{1}{2013}$-$\frac{1}{2013}$+$\frac{1}{2014}$
=1+$\frac{1}{2014}$
=$\frac{2015}{2014}$.
点评 考查了规律型:数字的变化类,此类规律题要分别找到等式左边和右边的规律,寻找不变的量和变化的量,本题中不变的量是分数中的分子1,负号“-”,变化的量是分数中分母,所以要从分母中找到变化的规律,从而找到这个等式的变化规律:-$\frac{1}{n}$×$\frac{1}{n+1}$=-$\frac{1}{n}$+$\frac{1}{n+1}$.


 学期复习一本通学习总动员期末加暑假延边人民出版社系列答案
学期复习一本通学习总动员期末加暑假延边人民出版社系列答案 芒果教辅暑假天地重庆出版社系列答案
芒果教辅暑假天地重庆出版社系列答案科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
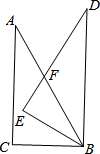 如图,△ABC中,∠C=90°,∠A=30°,AB=8,现将△ABC绕点B顺时针旋转30°至△DEB,DE交AB于点F,求线段DF的长.
如图,△ABC中,∠C=90°,∠A=30°,AB=8,现将△ABC绕点B顺时针旋转30°至△DEB,DE交AB于点F,求线段DF的长.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 已知:如图,在△ABC中,AD⊥BC,垂足为点D,BE⊥AC,垂足为点E,M为AB边的中点,连接ME、MD、ED.
已知:如图,在△ABC中,AD⊥BC,垂足为点D,BE⊥AC,垂足为点E,M为AB边的中点,连接ME、MD、ED.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com