
【题目】如图,在矩形纸片ABCD中,AB=4,AD=12,将矩形纸片折叠,使点C落在AD边上的点M处,折痕为PE,此时PD=3.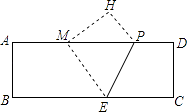
(1)求MP的值;
(2)在AB边上有一个动点F,且不与点A,B重合.当AF等于多少时,△MEF的周长最小?
(3)若点G,Q是AB边上的两个动点,且不与点A,B重合,GQ=2.当四边形MEQG的周长最小时,求最小周长值.(计算结果保留根号)
【答案】
(1)解:∵四边形ABCD为矩形,
∴CD=AB=4,∠D=90°,
∵矩形ABCD折叠,使点C落在AD边上的点M处,折痕为PE,
∴PD=PH=3,CD=MH=4,∠H=∠D=90°,
∴MP= ![]() =5
=5
(2)解:如图1,作点M关于AB的对称点M′,连接M′E交AB于点F,则点F即为所求,过点E作EN⊥AD,垂足为N,
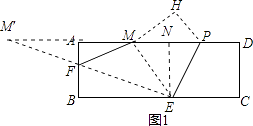
∵AM=AD﹣MP﹣PD=12﹣5﹣3=4,
∴AM=AM′=4,
∵矩形ABCD折叠,使点C落在AD边上的点M处,折痕为PE,
∴∠CEP=∠MEP,
而∠CEP=∠MPE,
∴∠MEP=∠MPE,
∴ME=MP=5,
在Rt△ENM中,MN= ![]() =
= ![]() =3,
=3,
∴NM′=11,
∵AF∥NE,
∴△AFM′∽△NEM′,
∴ ![]() =
= ![]() ,即
,即 ![]() =
= ![]() ,解得AF=
,解得AF= ![]() ,
,
即AF= ![]() 时,△MEF的周长最小
时,△MEF的周长最小
(3)解:如图2,由(2)知点M′是点M关于AB的对称点,在EN上截取ER=2,连接M′R交AB于点G,再过点E作EQ∥RG,交AB于点Q,
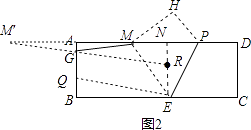
∵ER=GQ,ER∥GQ,
∴四边形ERGQ是平行四边形,
∴QE=GR,
∵GM=GM′,
∴MG+QE=GM′+GR=M′R,此时MG+EQ最小,四边形MEQG的周长最小,
在Rt△M′RN中,NR=4﹣2=2,
M′R= ![]() =5
=5 ![]() ,
,
∵ME=5,GQ=2,
∴四边形MEQG的最小周长值是7+5 ![]() .
.
【解析】(1)根据矩形的性质,四边形ABCD为矩形,得到CD=AB,∠D=90°,再由矩形ABCD折叠,使点C落在AD边上的点M处,折痕为PE,根据勾股定理得到MP的值;(2)根据折叠的性质,矩形ABCD折叠,使点C落在AD边上的点M处,折痕为PE,得到∠CEP=∠MEP,ME=MP,根据勾股定理求出MN、NM′的值,由AF∥NE,得到△AFM′∽△NEM′,从而求出AF的值,得到△MEF的周长最小;(3)由(2)知点M′是点M关于AB的对称点,得到四边形ERGQ是平行四边形,得到四边形MEQG的周长最小,根据勾股定理M′R的值,得到四边形MEQG的最小周长值.
【考点精析】本题主要考查了矩形的性质和轴对称-最短路线问题的相关知识点,需要掌握矩形的四个角都是直角,矩形的对角线相等;已知起点结点,求最短路径;与确定起点相反,已知终点结点,求最短路径;已知起点和终点,求两结点之间的最短路径;求图中所有最短路径才能正确解答此题.


科目:初中数学 来源: 题型:
【题目】(10分)某体育用品专卖店销售7个篮球和9个排球的总利润为355元,销售10个篮球和20个排球的总利润为650元.
(1)求每个篮球和每个排球的销售利润;
(2)已知每个篮球的进价为200元,每个排球的进价为160元,若该专卖店计划用不超过17400元购进篮球和排球共100个,且要求篮球数量不少于排球数量的一半,请你为专卖店设计符合要求的进货方案.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,点![]() 的坐标分别为
的坐标分别为![]() ,将线段
,将线段![]() 直接平移到
直接平移到![]() ,使点
,使点![]() 移至点
移至点![]() 的位置,点
的位置,点![]() 移至点
移至点![]() 的位置,设平移过程中线段
的位置,设平移过程中线段![]() 扫过的面积为
扫过的面积为![]() ,
,
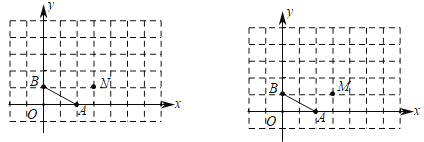
(1)如图1,若点![]() 的坐标是
的坐标是![]() ,则点
,则点![]() 的坐标为_____________,请画出平移后的线段
的坐标为_____________,请画出平移后的线段![]() ;
;
(2)如图2,若点![]() 的坐标是
的坐标是![]() ,请画出平移后的线段
,请画出平移后的线段![]() ,则
,则![]() 的值为_____________;
的值为_____________;
(3)若![]() ,且点
,且点![]() 在坐标轴上,请直接写出所有满足条件的
在坐标轴上,请直接写出所有满足条件的![]() 点的坐标.
点的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为了提高足球基本功,甲、乙、丙三位同学进行足球传球训练,球从一个人脚下随机传到另一个人脚下,且每位传球人传球给其余两人的机会是均等的,由甲开始传球,共传三次.
(1)请用树状图列举出三次传球的所有可能情况;
(2)三次传球后,球回到甲脚下的概率大还是传到乙脚下的概率大?
查看答案和解析>>
科目:初中数学 来源: 题型:
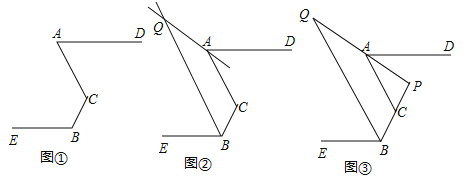
【题目】如图,已知:点![]() 不在同一条直线,
不在同一条直线,![]() .
.
(1)求证:![]() .
.
(2)如图②,![]() 分别为
分别为![]() 的平分线所在直线,试探究
的平分线所在直线,试探究![]() 与
与![]() 的数量关系;
的数量关系;
(3)如图③,在(2)的前提下,且有![]() ,直线
,直线![]() 交于点
交于点![]() ,
,![]() ,请直接写出
,请直接写出![]() ______________.
______________.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】阅读下面的学习材料(研学问题),尝试解决问题:
(a)某学习小组在学习时遇到如下问题:如图①,在Rt△ABC中,∠C=90°,D为边BC上一点,DA=DB,E为AD延长线上一点,∠AEB=120°,猜想BC、EA、EB的数量关系,并证明结论.大家经探究发现:过点B作BF⊥AE交AE的延长线于F,如图②所示,构造全等三角形使问题容易求解,请写出解答过程.
(b)参考上述思考问题的方法,解答下列问题:
如图③,等腰△ABC中,AB=AC,H为AC上一点,在BC的延长线上顺次取点E、F,在CB的延长线上取点BD,使EF=DB,过点E作EG∥AC交DH的延长线于点G,连接AF,若∠HDF+∠F=∠BAC.
(1)探究∠BAF与∠CHG的数量关系;
(2)请在图中找出一条和线段AF相等的线段,并证明你的结论.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】图象中所反映的过程是:小敏从家跑步去体育场,在那里锻炼了一阵后,又去早餐店吃早餐,然后散步走回家,其中![]() 表示时间,
表示时间,![]() 表示小敏离家的距离,根据图象提供的信息,以下说法错误的是( )
表示小敏离家的距离,根据图象提供的信息,以下说法错误的是( )
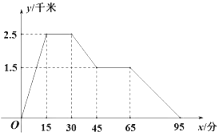
A. 体育场离小敏家2.5千米B. 体育场离早餐店4千米
C. 小敏在体育场锻炼了15分钟D. 小敏从早餐店回到家用时30分钟
查看答案和解析>>
科目:初中数学 来源: 题型:
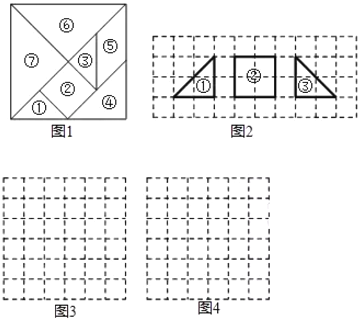
【题目】七巧板又称智慧板,是中国民间流传的智力玩具,它是由七块板组成(如图1),用这七块板可拼出许多图形(1600种以上),例如:三角形、平行四边形、以及不规则的多边形,它还可以拼出各种人物、动物、建筑等.请你用七巧板中标号为①②③的三块板(如图2经过平移、旋转拼出下列图形(相邻两块板之间无空隙,无重叠;示意图的顶点画在小方块顶点上):
(1)拼成长方形,在图3中画出示意图;
(2)拼成等腰直角三角形,在图4中面出示意图.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com