
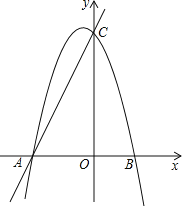
����Ŀ����ͼ����֪������L��y��ax2+bx+c��a��0����x�ύ��A��B���㣮��y�ύ��C�㣮��A����1��0����OB��OC��3OA��

��1����������L�ĺ�������ʽ��
��2����������L�ĶԳ������Ƿ����һ��M��ʹ��ACM�ܳ���С�������ڣ������M�����ꣻ�������ڣ���˵�����ɣ�
��3������AC��BC����������L���Ƿ����һ��N��ʹS��ABC��2S��OCN�������ڣ������N�����ꣻ�������ڣ���˵�����ɣ�
���𰸡���1��y��x2��2x��3����2�������߶Գ����ϴ��ڵ�M��1����2���������⣻��3�����������ĵ�N�������ǣ�2����3����2��5����
��������
��1�����ô���ϵ����ȷ����������ʽ���ɣ�
��2����B�ǵ�A���������߶Գ���ĶԳƵ㣬�������ߵĶԳ�������һ��M��ҪʹMA+MC��ֵ��С�����M����BC�������߶Գ���Ľ��㣬���ô���ϵ�������ֱ��BC�Ľ���ʽ���������߶Գ���r=1���뼴����⣻
��3����N��x��x2��2x��3�������������ε������ʽ���.
��1����A����1��0����OB��OC��3OA����
OB��OC��3��
��B��3��0����C��0����3����
��A��B��C��������뺯������ʽ����
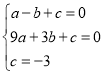 ��
��
��� ��
��
�����ߵĽ���ʽΪy��x2��2x��3��
��2������A��B���ڶԳ���Գƣ�
����MΪBC��Գ���Ľ���ʱ��MA+MC��ֵ��С��
��ֱ��BC�Ľ���ʽΪy��kx+t��k��0����
��![]() ��
��
��ã�![]() ��
��
��ֱ��AC�Ľ���ʽΪy��x��3��
�������ߵĶԳ���Ϊֱ��x��1��
����x��1ʱ��y����2��
�������߶Գ����ϴ��ڵ�M��1����2���������⣻
��3����N��x��x2��2x��3����
��A����1��0����B��3��0����
��AB��4��OC��3��
��S��ABC��![]() ABOC��
ABOC��![]() ��4��3��6��
��4��3��6��
��S��ABC��2S��OCN��
��2��![]() OC|x|��6����|x|��2��
OC|x|��6����|x|��2��
���x��2��x����2��
��x��2ʱ��x2��2x��3����3����ʱN��2����3����
��x����2ʱ��x2��2x��3��5����ʱN����2��5����
�������������������ĵ�N�������ǣ�2����3����2��5����


 �Ķ��쳵ϵ�д�
�Ķ��쳵ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪������y1��y��2��x��3��2+1��������y2��y����2x2��8x��3��������kȡ��ֵ��ֱ��y��kx+km+n���������������ص������߶ζ�������ȣ���m��_____��n��_____��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ�����ı���ABCD�У���B����C��90������AB��4��BC��4��CD��1���ʣ���BC���Ƿ���ڵ�P��ʹ��AP��PD�������ڣ����BP�ij����������ڣ���˵�����ɣ�
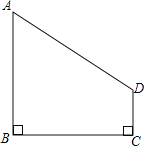
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ������������״��С��ȫ��ͬ���ƣ�����ֱ��������2��3��5���������Ʊ��泯�ϣ�ϴ�Ⱥ���������ϣ�
��1��������ȡһ�ţ���ȡ��ż���ĸ���.
��2���ס������˽���������Ϸ.
�ټ״��������ȡһ���ƣ���¼���ֺ�Ż�ϴ�ȣ����������ȡһ�ţ������б�������״ͼ�ķ����������˳�ȡ��ͬ���ֵĸ��ʣ�
�������˳�ȡ�����ֺ�Ϊ2�ı��������ʤ������ȡ�����ֺ�Ϊ5�ı��������һ�ʤ�������Ϸ��ƽ�����ø��ʵ�֪ʶ���Խ��ͣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����ƽ��ֱ������ϵ�У�OΪ����ԭ�㣬��A��3��0����B��3��4����

��1��������AOB��ԭ��O��ʱ����ת90���õ�����A'OB'����д����A'��B'�����ꣻ
��2�����߶�AB��������ת������ɨ�������������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����10�֣�ˮ�����Ű�����ÿ��2Ԫ�ļ۸�ij��ˮ�����ɽȻ����ÿ��4Ԫ�ļ۸���ۣ�ÿ����۳�100�ͨ�����鷢�֣�����ˮ��ÿ����ۼ�ÿ����0.1Ԫ��ÿ��ɶ��۳�20�Ϊ��֤ÿ�������۳�260��Ű��̾����������ۣ�
��1����������ˮ��ÿ����ۼ۽���xԪ����ÿ����������� ��ú�x�Ĵ���ʽ��ʾ����
��2����������ˮ��Ҫ��ÿ��ӯ��300Ԫ���Ű����轫ÿ����ۼ۽��Ͷ���Ԫ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����![]() �У�
��![]() ����
����![]() Ϊֱ����
Ϊֱ����![]() ����D��
����D��![]() �ϣ�
�ϣ�![]() ��
��![]() ��������E��
��������E��![]() ��
��![]() ��
��![]() �ֱ��ڵ�M��F������
�ֱ��ڵ�M��F������![]() ��
��![]() ��
��![]() ��
��

��1��֤����![]() ��
��![]() �����ߣ�
�����ߣ�
��2����![]() ��
��![]() ����
����![]() �İ뾶����
�İ뾶����
��3���ڣ�2���������£���![]() �ij���
�ij���
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ�����浹���ű���ͼ����ͬ�����ſ�Ƭ��������ֱ���������![]() ���������ȡһ�ţ���Ƭ�ϵ�������x�����Żأ��ٳ�ȡһ�ţ���Ƭ�ϵ����ּ���y�����A������Ϊ��x��y��.
���������ȡһ�ţ���Ƭ�ϵ�������x�����Żأ��ٳ�ȡһ�ţ���Ƭ�ϵ����ּ���y�����A������Ϊ��x��y��.
(1)����״ͼ���б����оٵ�A���е����������
(2)���A��������![]() �ϵĸ��ʣ�
�ϵĸ��ʣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��ʾ����ֱ֪��y��kx+m��x�ᡢy��ֱ���A��C���㣬������y����x2+bx+c����A��C���㣬��B����������x�����һ�����㣬��x����![]() ʱ��yȡ���ֵ
ʱ��yȡ���ֵ![]() ��
��
��1���������ߺ�ֱ�ߵĽ���ʽ��
��2�����P��ֱ��AC��һ�㣬��S��ABP��S��BPC��1��3�����P�����ꣻ
��3����ֱ��y��![]() x+a�루1��������������߽���M��N���㣬�ʣ�
x+a�루1��������������߽���M��N���㣬�ʣ�
���Ƿ����a��ֵ��ʹ�á�MON��90���������ڣ����a��ֵ���������ڣ���˵�����ɣ�
�ڲ��뵱��MON��90��ʱ��a��ȡֵ��Χ����д���̣�ֱ��д���ۣ���
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com