
【题目】如图,在![]() 中,
中,![]() ,以
,以![]() 为直径作
为直径作![]() ,点D在
,点D在![]() 上,
上,![]() ,
,![]() ,垂足为点E,
,垂足为点E,![]() 与
与![]() 和
和![]() 分别交于点M、F.连接
分别交于点M、F.连接![]() 、
、![]() 、
、![]() .
.

(1)证明:![]() 是
是![]() 的切线;
的切线;
(2)若![]() ,
,![]() ,求
,求![]() 的半径长;
的半径长;
(3)在(2)的条件下,求![]() 的长.
的长.
【答案】(1)证明见详解;(2)5;(3)2
【解析】
(1)易证BCOBDO,可得:∠BDO=∠BCO=90°,即:OD⊥BD,即可得证;
(2)由![]() ,得AE:ME:AM=1:2:
,得AE:ME:AM=1:2:![]() ,即AE=2,ME=4,连接CM,由tan∠ACM= tan∠AME=
,即AE=2,ME=4,连接CM,由tan∠ACM= tan∠AME=![]() ,可得:CM=
,可得:CM=![]() ,根据勾股定理得AC的长,即可得到结论;
,根据勾股定理得AC的长,即可得到结论;
(3)过点B作BN∥AC,交MD的延长线于点N,设EF=x,由AEF~BNF,得NF=4x,从而得BC=NE=5x,BD=BC=5x,DN=NE-DE=5x-4,根据勾股定理,求出x的值,进而得到答案.
(1)在BCO和BDO中,
∵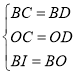
∴BCOBDO(SSS),
∴∠BDO=∠BCO=90°,即:OD⊥BD,
∴![]() 是
是![]() 的切线;
的切线;
(2)∵![]() ,
,
∴DE=ME,
∴AM=![]() ,
,
∵![]() ,
,
∴AE:ME:AM=1:2:![]() ,
,
∴AE=2,ME=4,
连接CM,则∠AMC=90°,
∵∠AME+∠CME=90°,
∠CME+∠ACM=90°,
∴∠AME=∠ACM,
∴tan∠ACM= tan∠AME=![]() ,
,
∴CM=2AM=2×![]() =
=![]() ,
,
∴AC=![]() ,
,
∴![]() 的半径长是:5.
的半径长是:5.
(3)过点B作BN∥AC,交MD的延长线于点N,
由(2)题可知:AE=2,EC=8,DE=ME=4,
∵四边形ECBN是矩形,
∴BN=EC=8,
设EF=x,
∵BN∥AC,
∴AEF~BNF,
∴![]() ,即:
,即:![]() ,
,
∴NF=4x,
∴BC=NE=5x,
∴BD=BC=5x,DN=NE-DE=5x-4,
∵在RtBND中,![]() ,
,
∴![]() ,解得:x=2,
,解得:x=2,
∴DF=DE-EF=4-2=2,


科目:初中数学 来源: 题型:
【题目】如图,在四边形ABCD中,AB=AD=6,AB⊥BC,AD⊥CD,∠BAD=60°,点M、N分别在AB、AD边上,若AM:MB=AN:ND=1:2.则∠BCD= °,cos∠MCN= .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知,如图,在矩形ABCD中,AB=8,BC=x(0<x≤8),点E在边CD上,且CE=CB,以AE为对角线作正方形AGEF.设正方形AGEF的面积y.
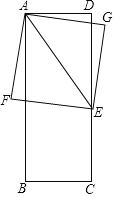
(1)当点F在矩形ABCD的边上时,x= .
(2)求y与x的函数关系式及y的取值范围.
(3)当矩形ABCD的一条边将正方形AGEF的面积分为1:3两部分时,直接写出x的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知抛物线L:y=ax2+bx+c(a≠0)与x轴交于A、B两点.与y轴交于C点.且A(﹣1,0),OB=OC=3OA.

(1)求抛物线L的函数表达式;
(2)在抛物线L的对称轴上是否存在一点M,使△ACM周长最小?若存在,求出点M的坐标;若不存在,请说明理由.
(3)连接AC、BC,在抛物线L上是否存在一点N,使S△ABC=2S△OCN?若存在,求出点N的坐标;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
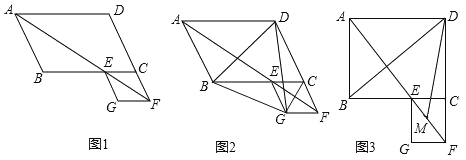
【题目】在ABCD中,∠BAD的平分线交直线BC于点E,交直线DC的延长线于点F,以EC、CF为邻边作ECFG.
(1)如图1,证明ECFG为菱形;
(2)如图2,若∠ABC=120°,连接BG、CG,并求出∠BDG的度数:
(3)如图3,若∠ABC=90°,AB=6,AD=8,M是EF的中点,求DM的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】深圳国际马拉松赛事设有A“全程马拉松”,B“半程马拉松”,C“嘉年华马拉松”三个项目,小智和小慧参加了该赛事的志愿者服务工作,组委会将志愿者随机分配到三个项目组.
(1)小智被分配到A“全程马拉松”项目组的概率为 .
(2)用树状图或列表法求小智和小慧被分到同一个项目标组进行志愿服务的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系xOy中,将点![]() 定义为点
定义为点![]() 的“关联点”. 已知点
的“关联点”. 已知点![]() 在函数
在函数![]() 的图像上,将点A的“关联点”记为点
的图像上,将点A的“关联点”记为点![]() .
.

(1)请在如图基础上画出函数![]() 的图像,简要说明画图方法;
的图像,简要说明画图方法;
(2)如果点![]() 在函数
在函数![]() 的图像上,求点
的图像上,求点![]() 的坐标;
的坐标;
(3)将点![]() 称为点
称为点![]() 的“待定关联点”(其中
的“待定关联点”(其中![]() ),如果点
),如果点![]() 的“待定关联点”
的“待定关联点”![]() 在函数
在函数![]() 的图像上,试用含
的图像上,试用含![]() 的代数式表示点
的代数式表示点![]() 的坐标.
的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
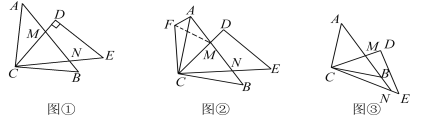
【题目】将两块斜边长相等的等腰直角三角板按如图①摆放,斜边AB分别交CD,CE于M,N点.
(1)如果把图①中的△BCN绕点C逆时针旋转90°得到△ACF,连接FM,如图②,求证:△CMF≌△CMN;
(2)将△CED绕点C旋转,则:
①当点M,N在AB上(不与点A,B重合)时,线段AM,MN,NB之间有一个不变的关系式,请你写出这个关系式,并说明理由;
②当点M在AB上,点N在AB的延长线上(如图③)时,①中的关系式是否仍然成立?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,B是![]() 的半径OA上的一点(不与端点重合),过点B作OA的垂线交
的半径OA上的一点(不与端点重合),过点B作OA的垂线交![]() 于点C,D,连接OD,E是
于点C,D,连接OD,E是![]() 上一点,
上一点,![]() ,过点C作
,过点C作![]() 的切线l,连接OE并延长交直线l于点F.
的切线l,连接OE并延长交直线l于点F.
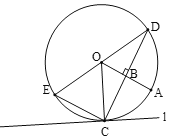
(1)①依题意补全图形.
②求证:∠OFC=∠ODC.
(2)连接FB,若B是OA的中点,![]() 的半径是4,求FB的长.
的半径是4,求FB的长.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com