
 如图,一正方体包装箱沿斜面坡角为30°的电梯上行,已知正方体包装箱的棱长为2米,电梯AB长为16米,当正方体包装箱的一个顶点到达电梯上端B时,求另一顶点C离地面的高度.(参考数据:$\sqrt{3}$≈1.73)
如图,一正方体包装箱沿斜面坡角为30°的电梯上行,已知正方体包装箱的棱长为2米,电梯AB长为16米,当正方体包装箱的一个顶点到达电梯上端B时,求另一顶点C离地面的高度.(参考数据:$\sqrt{3}$≈1.73) 分析 根据题意可以构造出适合的直角三角形,由一正方体包装箱沿斜面坡角为30°的电梯上行,已知正方体包装箱的棱长为2米,电梯AB长为16米,当正方体包装箱的一个顶点到达电梯上端B时,可以得到CD、BD的长,从而可以求得DM的长,从而可以求得另一顶点C离地面的高度.
解答 解:过点C作CM⊥AE,交AB于点D,交AE于点M,作BF⊥AE于点F,如下图所示,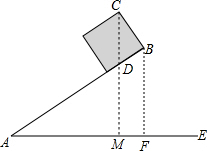
由题意可得,∠A=30°,AB=16,BC=2,
则∠DCB=30°,
∴BD=BC•tan30°=2×$\frac{\sqrt{3}}{3}$=$\frac{2\sqrt{3}}{3}$,CD=$\frac{BC}{cos30°}=\frac{2}{\frac{\sqrt{3}}{2}}=\frac{4\sqrt{3}}{3}$,
∴AD=AB-BD=16-$\frac{2\sqrt{3}}{3}$,
∴DM=AD•sin30°=(16-$\frac{2\sqrt{3}}{3}$)×$\frac{1}{2}$=8-$\frac{\sqrt{3}}{3}$,
∴CM=CD+DM=$\frac{4\sqrt{3}}{3}$+8-$\frac{\sqrt{3}}{3}$=8+$\sqrt{3}$,
即另一顶点C离地面的高度是(8+$\sqrt{3}$)米.
点评 本题考查解直角三角形的应用-坡度坡角问题,解题的关键是构造合适的直角三角形,利用锐角直角三角函数值求出相应的边的长度.


科目:初中数学 来源: 题型:解答题
 如图,E是正方形ABCD对角线延长线上一点,连接DE,作E作DE的垂线CB和BA的延长线分别交于F和G,判断△GDF的形状并证明你的结论.
如图,E是正方形ABCD对角线延长线上一点,连接DE,作E作DE的垂线CB和BA的延长线分别交于F和G,判断△GDF的形状并证明你的结论.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
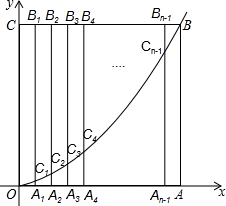 如图,边长为n的正方形OABC的边OA、OC分别在x轴和y轴的正半轴上,A1、A2、A3、…、An-1为OA的n等分点,B1、B2、B3、…Bn-1为CB的n等分点,连接A1B1、A2B2、A3B3、…、An-1Bn-1,分别交y=$\frac{1}{n}$x2(x≥0)于点C1、C2、C3、…、Cn-1,若有B5C5=3C5A5时,则n=10.
如图,边长为n的正方形OABC的边OA、OC分别在x轴和y轴的正半轴上,A1、A2、A3、…、An-1为OA的n等分点,B1、B2、B3、…Bn-1为CB的n等分点,连接A1B1、A2B2、A3B3、…、An-1Bn-1,分别交y=$\frac{1}{n}$x2(x≥0)于点C1、C2、C3、…、Cn-1,若有B5C5=3C5A5时,则n=10.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
 如图,小明要测量河内小岛B到河边公路l的距离,在A点测得∠BAD=30°,在C点测得∠BCD=60°,又测得AC=60米,则小岛B到公路l的距离为( )
如图,小明要测量河内小岛B到河边公路l的距离,在A点测得∠BAD=30°,在C点测得∠BCD=60°,又测得AC=60米,则小岛B到公路l的距离为( )| A. | 30米 | B. | 30$\sqrt{3}$米 | C. | 40$\sqrt{3}$米 | D. | (30+30$\sqrt{3}$)米 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com