
| һ���Թ�����ܽ�� | �Żݴ�ʩ |
| ������300Ԫ | ���Ż� |
| ����300Ԫ�Ҳ�����500Ԫ | �ۼ۴���� |
| ����500Ԫ | �ۼ۴���� |
���� ��1����һ������xԪ��һ������yԪ�����ݹ���2�������4��������420Ԫ������3�������1������Ҫ�70Ԫ���з�������⣻
��2���蹺������m������������30-m���������ݷ��ò�����1600Ԫ���в���ʽ��⣻
��3�����ݴ������߷ֱ��������������������ĸ�����
��� �⣺��1����һ������xԪ��һ������yԪ��
������ã�$\left\{\begin{array}{l}{2x+4y=420}\\{3x-y=70}\end{array}\right.$��
��ã�$\left\{\begin{array}{l}{x=50}\\{y=80}\end{array}\right.$��
��һ������50Ԫ��һ������80Ԫ��
��2���蹺������m������������30-m������
������ã�50m+80��30-m����1600��
��ã�m��$\frac{80}{3}$=26$\frac{2}{3}$��
��30-m��0��m��30��
��m��ȡֵΪ27��28��29��30��
�������ַ������ٹ�������27������������3����
�ڹ�������28������������2����
�۹�������29������������1����
�ܹ�������30������������0����
��3����һ�ι�������$\frac{200}{50}$=4����������һ�ι�������$\frac{360}{80��0.9}$=5��
��ڶ��ι�������a������������b����
��0.8��50a+80b��=560��
a=$\frac{70-8b}{5}$��
��a��b��������
�൱b=5ʱ��aΪ����6��
�ʵ�һ�ι�������4������������3����
�ڶ��ι�������6������������5����
���� ���⿼���˶�Ԫһ�η������һԪһ�β���ʽ��Ӧ�ã������Ĺؼ��Ƕ������⣬���δ֪�����ҳ����ʵĵ�����ϵ���з��̺Ͳ���ʽ��⣮


 53���ò�ϵ�д�
53���ò�ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
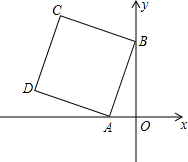 ��ͼ��A��-1��0����B��0��3������ABΪ����������ABCD����C��D�����꣮
��ͼ��A��-1��0����B��0��3������ABΪ����������ABCD����C��D�����꣮�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | $\frac{2}{x}$$\sqrt{x-a}$ | B�� | $\frac{2a}{{x}^{2}}$$\sqrt{x-a}$ | C�� | 2ax4$\sqrt{x-a}$ | D�� | $\frac{2a}{x}$$\sqrt{x-a}$ |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com