
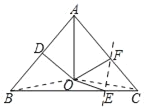
【题目】如图,在△ABC中,AB=AC,∠BAC=88°,∠BAC的平分线与AB的垂直平分线交于点O,点E、F分别在BC、AC上,点C沿EF折叠后与点O重合,则∠DOE的度数为_____.

【答案】140゜
【解析】
连接OB、OC,根据角平分线定义和线段垂直平分线的性质得到∠OAB=∠ABO=44°,再根据等腰三角形的性质得到∠ABC=∠ACB=46°,求出∠OBC=2°,由于AB=AC,OA平分∠BAC,根据等腰三角形的性质得OA垂直平分BC,则BO=OC,所以得出∠OBC=∠OCB=2°,然后根据折叠的性质得到EO=EC,于是∠OCB=∠EOC=2°,再根据三角形的外角性质得出∠OEB,求出∠BOE和∠BOD的度数,即可得出答案.
解:连接OB、OC,如图所示:
∵∠BAC=88°,∠BAC的平分线与AB的中垂线交于点O,
∴∠OAB=∠ABO=44°,
∵AB=AC,∠BAC=88°,
∴∠ABC=∠ACB=46°,
∴∠OBC=46°﹣44°=2°,
∵AB=AC,OA平分∠BAC,
∴OA垂直平分BC,
∴BO=OC,
∴∠OBC=∠OCB=2°,
∵点C沿EF折叠后与点O重合,
∴EO=EC,
∴∠OCB=∠EOC=2°,
∴∠OEB=∠OCB+∠EOC=4°,
∴∠BOE=180°﹣4°﹣2°=174°,
∵∠BOD=90°﹣44°=46°,
∴∠DOE=360°﹣46°﹣174°=140°,
故答案为:140°.


 名牌学校分层周周测系列答案
名牌学校分层周周测系列答案 黄冈海淀全程培优测试卷系列答案
黄冈海淀全程培优测试卷系列答案科目:初中数学 来源: 题型:
【题目】如图:在△ABC中,BE、CF分别是AC、AB两边上的高,在BE上截取BD=AC,在CF的延长线上截取CG=AB,连接AD、AG.
(1)求证:AD=AG;
(2)AD与AG的位置关系如何,请说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
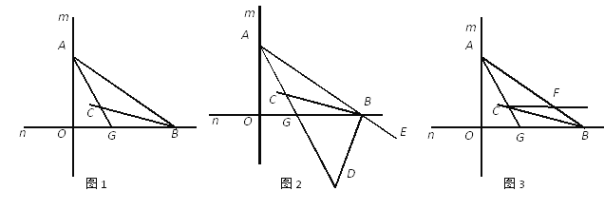
【题目】如图1,直线m与直线n垂直相交于O,点A在直线m上运动,点B 在直线n上运动,AC、BC分别是∠BAO和∠ABO的角平分线.
(1)求∠ACB的大小;
(2)如图2,若BD是△AOB的外角∠OBE的角平分线,BD与AC相交于点D,点A、B在运动的过程中,∠ADB的大小是否会发生变化?若发生变化,请说明理由;若不发生变化,试求出其值;
(3)如图3,过C作直线与AB交于F,且满足∠AGO-∠BCF=45°,求证:CF∥OB.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,过边长为2的等边△ABC的边AB上点P作PE⊥AC于E,Q为BC延长线上一点,当PA=CQ时,连PQ交AC边于D,则DE长为_____.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在Rt△ABC中,![]() ,
,![]() ,
,![]() ,CP、CM分别是AB上的高和中线,如果圆A是以点A为圆心,半径长为2的圆,那么下列判断正确的是( )
,CP、CM分别是AB上的高和中线,如果圆A是以点A为圆心,半径长为2的圆,那么下列判断正确的是( )
A. 点P,M均在圆A内 B. 点P、M均在圆A外
C. 点P在圆A内,点M在圆A外 D. 点P在圆A外,点M在圆A内
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,点D在AB上,点E在AC上,且∠AEB=∠ADC,那么补充下列一个条件后,仍无法判定△ABE≌△ACD的是( )

A.AD=AEB.∠B=∠CC.BE=CDD.AB=AC
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,由相同边长的小正方形组成的网格图形,A、B、C都在格点上,利用网格画图:(注:所画线条用黑色签字笔描黑)
(1)过点C画AB的平行线CF,标出F点;
(2)过点B画AC的垂线BG,垂足为点G,标出G点;
(3)点B到AC的距离是线段 的长度;
(4)线段BG、AB的大小关系为:BG AB(填“>”、“<”或“=”),理由是 .

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某校开设了足球、篮球、乒乓球和羽毛球四个课外体育活动小组,有512名学生参加,每人只参加一个组.为了了解学生参与的情况,对参加的人员分布情况进行抽样调查,并绘制了下面两幅不完整的统计图,请根据图中提供信息,解答下面问题:

(1)此次共抽查了多少名同学?
(2)将条形统计图补充完整;在扇形统计图中的括号中填写百分数;
(3)请估计该校参加篮球运动小组的学生人数
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com