
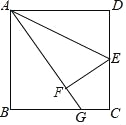
【题目】如图,在矩形ABCD中,点E是边CD的中点,将△ADE沿AE折叠后得到△AFE,且点F在矩形ABCD的内部,将AF延长后交边BC于点G,且![]() ,则
,则![]() 的值为__.
的值为__.
【答案】![]()
【解析】
根据中点定义可得DE=CE,再根据翻折的性质可得DE=EF,AF=AD,∠AFE=∠D=90°,从而得到CE=EF,连接EG,利用“HL”证明Rt△ECG和Rt△EFG全等,根据全等三角形对应边相等可得CG=FG,设CG=a,表示出GB,然后求出BC,再根据矩形的对边相等可得AD=BC,从而求出AF,再求出AG,然后利用勾股定理求出AB,再求比值即可.
解:如图,连接GE.
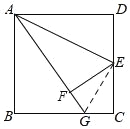
∵四边形ABCD是矩形,∴AD=BC.
∵点E是边CD的中点,∴DE=CE.
∵将△ADE沿AE折叠后得到△AFE,∴DE=EF,AF=AD,∠AFE=∠D=90°,∴CE=EF.在Rt△ECG和Rt△EFG中,![]() ,
,
∴Rt△ECG≌Rt△EFG(HL),
∴CG=FG.
∵![]() =
=![]() ,
,
∴设CG=2a=FG,BC=7a,
∴BG=5a,AD=AF=7a,
∴AG=9a.
在Rt△ABG中,AB=![]() =
=![]() a,
a,
∴![]() =
=![]() .
.
故答案为:![]() .
.


科目:初中数学 来源: 题型:
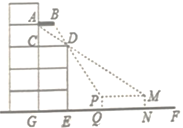
【题目】周末,小凯和同学带着皮尺,去测量杨大爷家露台遮阳蓬的宽度,如图,由于无法直接测量,小凯便在楼前面的地面上选择了一条直线EF,通过在直线EF上选点观测,发现当他位于N点时,他的视线从M点通过露台D点正好落在遮阳蓬A点处:当他位于Q点时,视线从P点通过露台D点正好落在遮阳蓬B点处,这样观测到两个点A,B间的距离即为遮阳蓬的宽.已知AB∥CD∥EF,点C在AG上,AG、DE、PQ、MN均为垂直于EF,MN=PQ,露台的宽CD=GE,测得GE=5米,EN=13.2米,QN=6.2,请你根据以上信息,求出遮阳蓬的宽AB是多少米?(结果精确到0.01米)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系中,抛物线y=ax2﹣3(a+1)x+2a+3(a≠0)与直线y=x﹣1交于点A和点B(点A在点B的左侧),AB=5![]() .
.
(1)求证:该抛物线必过一个定点;
(2)求该抛物线的解析式;
(3)设直线x=m与该抛物线交于点E(x1,y1),与直线AB交于点F(x2,y2),当满足y1+y2>0且y1y2<0时,求m的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知等边△ABC的边长为8,以AB为直径的圆交BC于点F.以C为圆心,CF长为半径作图,D是⊙C上一动点,E为BD的中点,当AE最大时,BD的长为( )

A. ![]() B.
B. ![]() C.
C. ![]() D. 12
D. 12
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】问题发现:
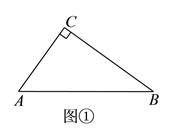
(![]() )如图①,
)如图①,![]() 中,
中,![]() ,
,![]() ,
,![]() ,点
,点![]() 是
是![]() 边上任意一点,则
边上任意一点,则![]() 的最小值为__________.
的最小值为__________.
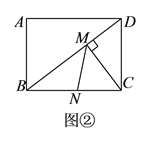
(![]() )如图②,矩形
)如图②,矩形![]() 中,
中,![]() ,
,![]() ,点
,点![]() 、点
、点![]() 分别在
分别在![]() 、
、![]() 上,求
上,求![]() 的最小值.
的最小值.
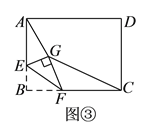
(![]() )如图③,矩形
)如图③,矩形![]() 中,
中,![]() ,
,![]() ,点
,点![]() 是
是![]() 边上一点,且
边上一点,且![]() ,点
,点![]() 是
是![]() 边上的任意一点,把
边上的任意一点,把![]() 沿
沿![]() 翻折,点
翻折,点![]() 的对应点为点
的对应点为点![]() ,连接
,连接![]() 、
、![]() ,四边形
,四边形![]() 的面积是否存在最小值,若存在,求这个最小值及此时
的面积是否存在最小值,若存在,求这个最小值及此时![]() 的长度;若不存在,请说明理由.
的长度;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,有长为 24m 的篱笆,现一面利用墙(墙的最大可用长度 a 为 10m)围成中间隔有一道篱笆的长方形花圃,设花圃的宽 AB 为 xm,面积为 Sm2.
(1) 求 S 与 x 的函数关系式及 x 值的取值范围;
(2) 要围成面积为 45m2 的花圃,AB 的长是多少米?
(3) 当 AB 的长是多少米时,围成的花圃的面积最大?

查看答案和解析>>
科目:初中数学 来源: 题型:
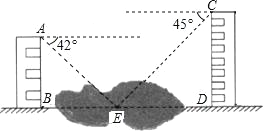
【题目】如图,两幢建筑物AB和CD,AB⊥BD,CD⊥BD,AB=15m,CD=20m.AB和CD之间有一景观池,小双在A点测得池中喷泉处E点的俯角为42°,在C点测得E点的俯角为45°,点B、E、D在同一直线上.求两幢建筑物之间的距离BD.(结果精确到0.1m)(参考数据:sin42°=0.67,cos42°=0.74,tan42°=0.90)
查看答案和解析>>
科目:初中数学 来源: 题型:
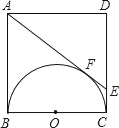
【题目】如图,正方形ABCD的边长为4cm,以正方形的一边BC为直径在正方形ABCD内作半圆,再过点A作半圆的切线,与半圆切于点F,与CD交于点E,则S梯形ABCE=_____cm2.
查看答案和解析>>
科目:初中数学 来源: 题型:
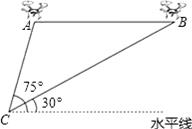
【题目】某兴趣小组借助无人飞机航拍校园.如图,无人飞机从A处水平飞行至B处需8秒,在地面C处同一方向上分别测得A处的仰角为75°,B处的仰角为30°.已知无人飞机的飞行速度为4米/秒,求这架无人飞机的飞行高度.(结果保留根号)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com