
分析 先将等式右边化为0,再对左边进行因式分解.
解答 解:∵a($\frac{1}{b}$+$\frac{1}{c}$)+b($\frac{1}{c}$+$\frac{1}{a}$)+c($\frac{1}{a}$+$\frac{1}{b}$)=-3,
∴a($\frac{1}{b}$+$\frac{1}{c}$)+b($\frac{1}{c}$+$\frac{1}{a}$)+c($\frac{1}{a}$+$\frac{1}{b}$)+3=0,
∴$\frac{a}{b}+\frac{a}{c}+\frac{b}{a}+\frac{b}{c}+\frac{c}{a}+\frac{c}{b}+\frac{a}{a}+\frac{b}{b}+\frac{c}{c}=0$,
∴$\frac{1}{a}(a+b+c)+\frac{1}{b}(a+b+c)+\frac{1}{c}(a+b+c)=0$,
∴$(a+b+c)(\frac{1}{a}+\frac{1}{b}+\frac{1}{c})=0$,
∵$\frac{1}{a}+\frac{1}{b}+\frac{1}{c}≠0$,
∴a+b+c=0.
点评 此题考查了代数式的恒等变形,将已知等式进行适当的变形变成若干个因式之积等于0的形式是本题的关键.


科目:初中数学 来源: 题型:解答题
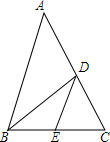 如图,在△ABC中,若$\frac{AB}{AD}$=$\frac{BC}{CD}$,AB=9,BC=6,DE∥AB,则△DCE的面积与四边形ABED的面积比是多少?
如图,在△ABC中,若$\frac{AB}{AD}$=$\frac{BC}{CD}$,AB=9,BC=6,DE∥AB,则△DCE的面积与四边形ABED的面积比是多少?查看答案和解析>>
科目:初中数学 来源: 题型:选择题
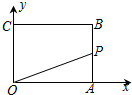 如图,已知矩形OABC,A(4,0),C(0,4),动点P从点A出发,沿A-B-C-O的路线匀速运动,设动点P的运动路程为t,△OAP的面积为S,则下列能大致反映S与t之间关系的图象是( )
如图,已知矩形OABC,A(4,0),C(0,4),动点P从点A出发,沿A-B-C-O的路线匀速运动,设动点P的运动路程为t,△OAP的面积为S,则下列能大致反映S与t之间关系的图象是( )| A. |  | B. |  | C. | 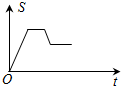 | D. | 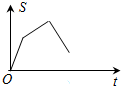 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
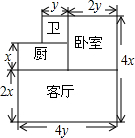 如图是一所住宅的建筑平面图(图中长度单位:m).
如图是一所住宅的建筑平面图(图中长度单位:m).查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com