
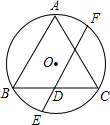
 如图,△ABC是⊙O的内接正三角形,弦EF经过BC边的中点D,且EF∥AB,若AB=8,则DE的长为( )
如图,△ABC是⊙O的内接正三角形,弦EF经过BC边的中点D,且EF∥AB,若AB=8,则DE的长为( )| A. | $\sqrt{5}$+1 | B. | 2$\sqrt{5}$-2 | C. | 2$\sqrt{3}$-2 | D. | $\sqrt{3}$+1 |
 口算题卡加应用题集训系列答案
口算题卡加应用题集训系列答案科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
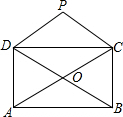 如图,矩形ABCD的对角线相交于点O,PD∥AC,PC∥BD.
如图,矩形ABCD的对角线相交于点O,PD∥AC,PC∥BD.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
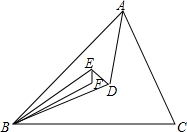 如图,△ABC内一点D,AD、BD、CD分别平分∠A、∠B、∠C,又E是△ABD内一点,AE、BE、CE分别平分△ABD各内角,F为△BDE内一点,BF、EF、DF分别平分△BDE各内角.若∠BFE的度数为整数,则∠BFE至少是113°度.
如图,△ABC内一点D,AD、BD、CD分别平分∠A、∠B、∠C,又E是△ABD内一点,AE、BE、CE分别平分△ABD各内角,F为△BDE内一点,BF、EF、DF分别平分△BDE各内角.若∠BFE的度数为整数,则∠BFE至少是113°度.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
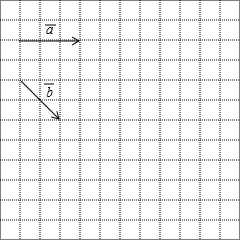 如图,在正方形网格中,每一个小正方形的边长都是1,已知向量$\overrightarrow{a}$和$\overrightarrow{b}$的起点、终点都是小正方形的顶点,如果$\overrightarrow{c}$=3$\overrightarrow{a}$-$\frac{1}{2}$$\overrightarrow{b}$,求作$\overrightarrow{c}$并写出$\overrightarrow{c}$的模(不用写作法,只要所求作向量).
如图,在正方形网格中,每一个小正方形的边长都是1,已知向量$\overrightarrow{a}$和$\overrightarrow{b}$的起点、终点都是小正方形的顶点,如果$\overrightarrow{c}$=3$\overrightarrow{a}$-$\frac{1}{2}$$\overrightarrow{b}$,求作$\overrightarrow{c}$并写出$\overrightarrow{c}$的模(不用写作法,只要所求作向量).查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 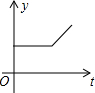 | B. | 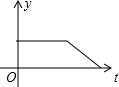 | C. | 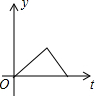 | D. |  |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,已知:AB∥CD,E、F分别是AB和CD上的点,DE、AF分别交BC于点G、H,∠A=∠D,试说明:
如图,已知:AB∥CD,E、F分别是AB和CD上的点,DE、AF分别交BC于点G、H,∠A=∠D,试说明:查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 高铁和特快两列火车分别从相距1000千米路程的甲、乙两地同时出发,先相向而行,高铁到达乙地后,停留1小时,然后按原路原速返回,高铁比特快晚1小时到达甲地,高铁和特快两列火车距甲地的路程y(千米)与出发后所用的时间x(小时)的关系如图所示,假定这两列火车均匀速行驶.
高铁和特快两列火车分别从相距1000千米路程的甲、乙两地同时出发,先相向而行,高铁到达乙地后,停留1小时,然后按原路原速返回,高铁比特快晚1小时到达甲地,高铁和特快两列火车距甲地的路程y(千米)与出发后所用的时间x(小时)的关系如图所示,假定这两列火车均匀速行驶.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com