
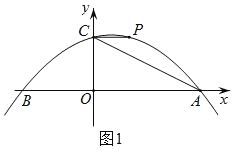
【题目】如图1,在平面直角坐标系中,抛物线y=![]() x2+
x2+![]() x+3与x轴交于A、B两点(点A在点B的右侧),与y轴交于点C,过点C作x轴的平行线交抛物线于点P.连接AC.
x+3与x轴交于A、B两点(点A在点B的右侧),与y轴交于点C,过点C作x轴的平行线交抛物线于点P.连接AC.
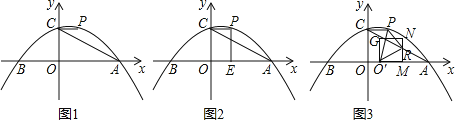
(1)求点P的坐标及直线AC的解析式;
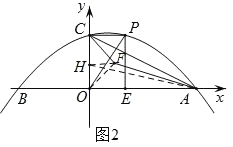
(2)如图2,过点P作x轴的垂线,垂足为E,将线段OE绕点O逆时针旋转得到OF,旋转角为α(0°<α<90°),连接FA、FC.求AF+![]() CF的最小值;
CF的最小值;
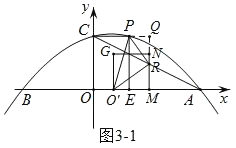
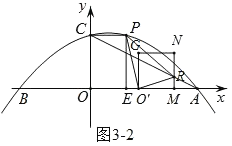
(3)如图3,点M为线段OA上一点,以OM为边在第一象限内作正方形OMNG,当正方形OMNG的顶点N恰好落在线段AC上时,将正方形OMNG沿x轴向右平移,记平移中的正方形OMNG为正方形O′MNG,当点M与点A重合时停止平移.设平移的距离为t,正方形O′MNG的边MN与AC交于点R,连接O′P、O′R、PR,是否存在t的值,使△O′PR为直角三角形?若存在,求出t的值;若不存在,请说明理由.
【答案】(1)P(2,3),yAC=﹣![]() x+3;(2)
x+3;(2)![]() ;(3)存在,t的值为
;(3)存在,t的值为![]() ﹣3或
﹣3或![]() ,理由见解析
,理由见解析
【解析】
(1)由抛物线y=![]() x2+
x2+![]() x+3可求出点C,P,A的坐标,再用待定系数法,可求出直线AC的解析式;
x+3可求出点C,P,A的坐标,再用待定系数法,可求出直线AC的解析式;
(2)在OC上取点H(0,![]() ),连接HF,AH,求出AH的长度,证△HOF∽△FOC,推出HF=
),连接HF,AH,求出AH的长度,证△HOF∽△FOC,推出HF=![]() CF,由AF+
CF,由AF+![]() CF=AF+HF≥AH,即可求解;
CF=AF+HF≥AH,即可求解;
(3)先求出正方形的边长,通过△ARM∽△ACO将相关线段用含t的代数式表示出来,再分三种情况进行讨论:当∠O'RP=90°时,当∠PO'R=90°时,当∠O'PR=90°时,分别构造相似三角形,即可求出t的值,其中第三种情况不存在,舍去.
(1)在抛物线y=![]() x2+
x2+![]() x+3中,
x+3中,
当x=0时,y=3,
∴C(0,3),
当y=3时,x1=0,x2=2,
∴P(2,3),
当y=0时,则![]() x2+
x2+![]() x+3=0,
x+3=0,
解得:x1=﹣4,x2=6,
B(﹣4,0),A(6,0),
设直线AC的解析式为y=kx+3,
将A(6,0)代入,
得,k=﹣![]() ,
,
∴y=﹣![]() x+3,
x+3,
∴点P坐标为P(2,3),直线AC的解析式为y=﹣![]() x+3;
x+3;
(2)在OC上取点H(0,![]() ),连接HF,AH,
),连接HF,AH,
则OH=![]() ,AH=
,AH=![]() ,
,
∵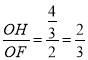 ,
,![]() ,且∠HOF=∠FOC,
,且∠HOF=∠FOC,
∴△HOF∽△FOC,
∴![]() ,
,
∴HF=![]() CF,
CF,
∴AF+![]() CF=AF+HF≥AH=
CF=AF+HF≥AH=![]() ,
,
∴AF+![]() CF的最小值为
CF的最小值为![]() ;
;
(3)∵正方形OMNG的顶点N恰好落在线段AC上,
∴GN=MN,
∴设N(a,a),
将点N代入直线AC解析式,
得,a=﹣![]() a+3,
a+3,
∴a=2,
∴正方形OMNG的边长是2,
∵平移的距离为t,
∴平移后OM的长为t+2,
∴AM=6﹣(t+2)=4﹣t,
∵RM∥OC,
∴△ARM∽△ACO,
∴![]() ,
,
即![]() ,
,
∴RM=2﹣![]() t,
t,
如图3﹣1,当∠O'RP=90°时,延长RN交CP的延长线于Q,
∵∠PRQ+∠O'RM=90°,∠RO'M+∠O'RM=90°,
∴∠PRQ=∠RO'M,
又∵∠Q=∠O'MR=90°,
∴△PQR∽△RMO',
∴![]() ,
,
∵PQ=2+t-2=t,QR=3﹣RM=1+![]() t,
t,
∴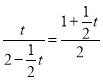 ,
,
解得,t1=﹣3﹣![]() (舍去),t2=
(舍去),t2=![]() ﹣3;
﹣3;
如图3﹣2,当∠PO'R=90°时,
∵∠PO'E+∠RO'M=90°,∠PO'E+∠EPO'=90°,
∴∠RO'M=∠EPO',
又∵∠PEO'=∠O'MR=90°,
∴△PEO'∽△O'MR,
∴![]() ,
,
即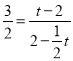 ,
,
解得,t=![]() ;
;
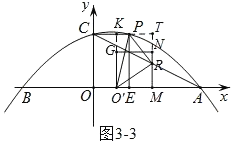
如图3﹣3,当∠O'PR=90°时,延长O’G交CP于K,延长MN交CP的延长线于点T,
∵∠KPO'+∠TPR=90°,∠KO'P+∠KPO'=90°,
∴∠KO'P=∠TPR,
又∵∠O'KP=∠T=90°,
∴△KO'P∽△TPR,
∴![]() ,
,
即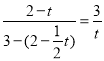 ,
,
整理,得t2-![]() t+3=0,
t+3=0,
∵△=b2﹣4ac=﹣![]() <0,
<0,
∴此方程无解,故不存在∠O'PR=90°的情况;
综上所述,△O′PR为直角三角形时,t的值为![]() ﹣3或
﹣3或![]() .
.


 名校课堂系列答案
名校课堂系列答案科目:初中数学 来源: 题型:
【题目】已知一个矩形纸片![]() ,将该纸片放置在平面直角坐标系中,点
,将该纸片放置在平面直角坐标系中,点![]() ,点
,点![]() ,点P为
,点P为![]() 边上的动点.
边上的动点.
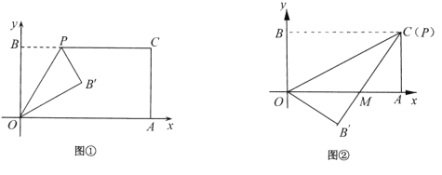
(1)如图①,经过点O、P折叠该纸片,得点![]() 和折痕
和折痕![]() .当点P的坐标为
.当点P的坐标为![]() 时,求
时,求![]() 的度数;
的度数;
(2)如图②,当点P与点C重合时,经过点O、P折叠纸片,使点B落在点![]() 的位置,
的位置,![]() 与
与![]() 交于点M,求点M的坐标;
交于点M,求点M的坐标;
(3)过点P作直线![]() ,交
,交![]() 于点Q,再取
于点Q,再取![]() 中点T,
中点T,![]() 中点N,分别以
中点N,分别以![]() ,
,![]() ,
,![]() ,
,![]() 为折痕,依次折叠该纸片,折叠后点O的对应点与点B的对应点恰好重合,且落在线段
为折痕,依次折叠该纸片,折叠后点O的对应点与点B的对应点恰好重合,且落在线段![]() 上,A、C的对应点也恰好重合,也落在线段
上,A、C的对应点也恰好重合,也落在线段![]() 上,求此时点P的坐标(直接写出结果即可).
上,求此时点P的坐标(直接写出结果即可).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在绿化某县城与高速公路的连接路段中,需购买罗汉松、雪松两种树苗共400株,罗汉松树苗每株60元,雪松树苗每株70元.相关资料表明:罗汉松、雪松树苗的成活率分别为70%,90%.
(1)若购买这两种树苗共用去26500元,则罗汉松、雪松树苗各购买多少株?
(2)绿化工程来年一般都要将死树补上新苗,现要使该两种树苗来年共补苗不多于80株,则罗汉松树苗至多购买多少株?
(3)在(2)的条件下,应如何选购树苗,才能使购买树苗的费用最低?请求出最低费用.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在矩形ABCD中,已知AB=2 ![]() ,AD=2,点P是对角线BD上一动点(不与B,D重合),连接AP,过点P作PE⊥AP,交DC于点E,
,AD=2,点P是对角线BD上一动点(不与B,D重合),连接AP,过点P作PE⊥AP,交DC于点E,
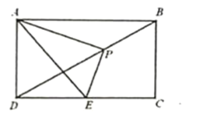
(1)求证:∠PAD=∠PEC;
(2)当点P是BD的中点时,求DE的值;
(3)在点P运动过程中,当DE= ![]() 时,求BP的值.
时,求BP的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某校“心灵信箱”的设立,为师、生之间的沟通开设了一个书面交流的渠道.为了解九年级学生对“心灵信箱”开通两年来的使用情况,某课题组对该校九年级全体学生进行了一次问卷调查,并根据调查结果绘制了如下尚不完整的统计图.
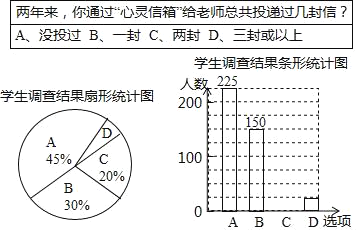
根据图表,解答以下问题:
(1)该校九年级学生共有 人;
(2)学生调查结果扇形统计图中,扇形D的圆心角度数是 ;
(3)请你补充条形统计图;
(4)根据调查结果可以推断:两年来,该校九年级学生通过“心灵信箱”投递出的信件总数至少有 封.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】观察下列各式规律:① 52-22=3×7;②72-42=3×11;③ 92-62=3×11;…;根据上面等式的规律:
(1)写出第6个和第n个等式;
(2)证明你写的第n个等式的正确性.
查看答案和解析>>
科目:初中数学 来源: 题型:
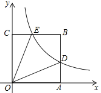
【题目】平面直角坐标系中,正方形OABC如图放置,反比例函数![]() 的图像交AB于点D,交BC于点E,已知A(
的图像交AB于点D,交BC于点E,已知A(![]() ,0),∠DOE=30°,则k的值为( )
,0),∠DOE=30°,则k的值为( )
A.![]() B.
B.![]() C.3D.3
C.3D.3![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
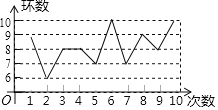
【题目】2019年第七届世界军人运动会(7thCISMMilitaryWorldGames)于2019年10月18日至27日在中国武汉举行,这是中国第一次承办综合性国际军事赛事,也是继北京奥运会后,中国举办的规模最大的国际体育盛会.某射击运动员在一次训练中射击了10次,成绩如图所示.下列结论中不正确的有( )个
①众数是8;②中位数是8;③平均数是8;④方差是1.6.
A.1B.2C.3D.4
查看答案和解析>>
科目:初中数学 来源: 题型:
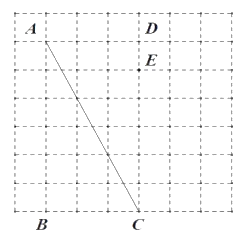
【题目】如图是由边长为![]() 的小正方形构成的网格,每个小正方形的顶点叫做格点.四边形
的小正方形构成的网格,每个小正方形的顶点叫做格点.四边形![]() 的顶点在格点上,点
的顶点在格点上,点![]() 是边
是边![]() 边上的一点.请选择适当的格点,用无刻度的直尺在网格中完成下列画图,保留连线的痕迹,不要求说明理由.
边上的一点.请选择适当的格点,用无刻度的直尺在网格中完成下列画图,保留连线的痕迹,不要求说明理由.
(1)①过![]() 作
作![]() 交
交![]() 边于
边于![]() ;
;
②过![]() 作
作![]() 于
于![]() 点;
点;
③在![]() 上作线段
上作线段![]()
(2)在(1)的条件下,连![]() ,若
,若![]() 为
为![]() 边上的动点,在网格中求作一条线段
边上的动点,在网格中求作一条线段![]() 等于
等于![]() 的最小值.
的最小值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com