
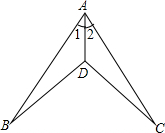
 如图,∠1=∠2,由SAS判定△ABD≌△ACD,则需添加的条件
如图,∠1=∠2,由SAS判定△ABD≌△ACD,则需添加的条件科目:初中数学 来源: 题型:
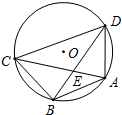 如图,已知A、B、C、D是⊙O上的四个点,AB=BC,BD交AC于点E,连接CD、AD.
如图,已知A、B、C、D是⊙O上的四个点,AB=BC,BD交AC于点E,连接CD、AD.查看答案和解析>>
科目:初中数学 来源: 题型:
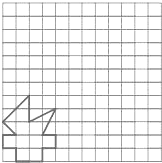 为迎接2009年10月11日第十一届全运会,山东体育迷小强利用网格设计了一个“火炬”图案,请你帮帮他:将“火炬”图案先向右平移7格,再向上平移6格,画出平移后的图案.
为迎接2009年10月11日第十一届全运会,山东体育迷小强利用网格设计了一个“火炬”图案,请你帮帮他:将“火炬”图案先向右平移7格,再向上平移6格,画出平移后的图案.查看答案和解析>>
科目:初中数学 来源: 题型:
| AB |
| AC |
| 3 |
| 1 |
| 2 |
| 1 |
| x |
| 4 |
| y |
| A、20 | B、18 | C、16 | D、9 |
查看答案和解析>>
科目:初中数学 来源: 题型:

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com