
 已知:在梯形ABCD中,AD∥BC,E、F分别是BD、AC中点,求证:EF∥BC,EF=$\frac{1}{2}$(BC-AD).
已知:在梯形ABCD中,AD∥BC,E、F分别是BD、AC中点,求证:EF∥BC,EF=$\frac{1}{2}$(BC-AD). 分析 首先连接DF,并延长交BC于点G,易证得△ADF≌△CGF(ASA),即可求得DF=GF,CG=AD,继而可得EF是△DBG的中位线,则可推知结论.
解答 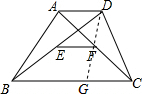 证明:连接DF,并延长交BC于点G,
证明:连接DF,并延长交BC于点G,
∵AD∥BC,
∴∠DAF=∠GCF,
在△ADF和△GCF中,$\left\{\begin{array}{l}{∠DAF=∠GCF}\\{AF=CF}\\{∠AFD=∠CFG}\end{array}\right.$,
∴△ADF≌△CGF(ASA),
∴DF=FG,CG=AD,
∴BG=BC-CG,
∵BE=DE,
∴EF=$\frac{1}{2}$BG=$\frac{1}{2}$(BC-AD),即EF=$\frac{1}{2}$(BC-AD).
点评 此题考查了梯形的性质、全等三角形的判定与性质以及三角形的中位线的性质.注意掌握辅助线的作法,注意掌握数形结合思想的应用.


 浙大优学小学年级衔接导与练浙江大学出版社系列答案
浙大优学小学年级衔接导与练浙江大学出版社系列答案 小学暑假作业东南大学出版社系列答案
小学暑假作业东南大学出版社系列答案 津桥教育暑假拔高衔接广东人民出版社系列答案
津桥教育暑假拔高衔接广东人民出版社系列答案 波波熊暑假作业江西人民出版社系列答案
波波熊暑假作业江西人民出版社系列答案科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
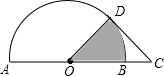 如图,AB为半圆O的直径,点C在AB的延长线上,CD与半圆O相切于点D,且AB=2CD=4,则图中阴影部分的面积为$\frac{π}{2}$.
如图,AB为半圆O的直径,点C在AB的延长线上,CD与半圆O相切于点D,且AB=2CD=4,则图中阴影部分的面积为$\frac{π}{2}$.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
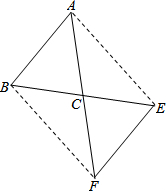 如图,在△ABC中,AB=AC,若将△ABC绕点C顺时针旋转180°得到△FEC.
如图,在△ABC中,AB=AC,若将△ABC绕点C顺时针旋转180°得到△FEC.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com