
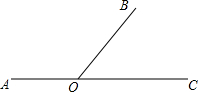
 如图,A、O、C在同一直线上,
如图,A、O、C在同一直线上,分析 (1)利用基本作图(作已知角的平分线)可作出OD、OE分别平分∠AOB、∠COB;
(2)根据角平分线的定义得到∠BOE=$\frac{1}{2}$∠BOC=23°,再利用邻补角得到∠AOB=134°,接着根据角平分线定义得∠AOD=∠BOD=$\frac{1}{2}$∠AOB=67°,然后计算∠BOD+∠BOE得到∠DOE的度数;
(3)利用角平分线定义和邻补角可证明∠BOE+∠BOD=90°,然后利用互余计算∠BOE的度数.
解答 解:(1)如图,OD、OE为所作;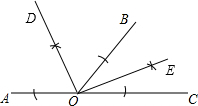
(2)∵OE平分∠BOC,
∴∠BOE=$\frac{1}{2}$∠BOC=$\frac{1}{2}$×46°=23°,
∵A、O、C在同一直线上,
∴∠AOB=180°-46°=134°,
∵OD平分∠AOD,
∴∠AOD=∠BOD=$\frac{1}{2}$∠AOB=67°,
∴∠DOE=∠BOD+∠BOE=67°+23°=90°;
故答案为23,67,90;
(3)∵∠BOE=$\frac{1}{2}$∠BOC,∠BOD=$\frac{1}{2}$∠AOB,
∴∠BOE+∠BOD=$\frac{1}{2}$×180°=90°,
∴∠BOE=90°-∠BOD=90°-56°=34°.
点评 本题考查了作图-基本作图:基本作图有:作一条线段等于已知线段;作一个角等于已知角;作已知线段的垂直平分线;作已知角的角平分线;过一点作已知直线的垂线.


 中考利剑中考试卷汇编系列答案
中考利剑中考试卷汇编系列答案 教育世家状元卷系列答案
教育世家状元卷系列答案 黄冈课堂作业本系列答案
黄冈课堂作业本系列答案 单元加期末复习先锋大考卷系列答案
单元加期末复习先锋大考卷系列答案科目:初中数学 来源: 题型:选择题
| A. | 0.13×1012 | B. | 1.3×1011 | C. | 1.3×1012 | D. | 13×1011 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
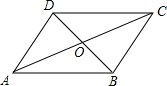 在2013年“植树月“的活动中,某校为了绿化校园,决定修建一个平行四边形花园(如图所示,图中的线段代表小路).已知D0=BO=5m,AC=26m,∠ADB=90°,求小路BC的长和花园的面积.
在2013年“植树月“的活动中,某校为了绿化校园,决定修建一个平行四边形花园(如图所示,图中的线段代表小路).已知D0=BO=5m,AC=26m,∠ADB=90°,求小路BC的长和花园的面积.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com