
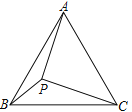
【题目】如图,在等边△ABC中,AC=7,点P在△ABC内部,且∠APC=90°,∠BPC=120°,则△APC的面积为___________
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:
【题目】我们给出如下定义:若一个四边形中存在相邻两边的平方和等于一条对角线的平方,则称这个四边形为勾股四边形,这两条相邻的边称为这个四边形的勾股边.
(1)写出你所学过的特殊四边形中是勾股四边形的一种图形的名称 ;
(2)如图 1,已知格点(小正方形的顶点)O(0,0),A(3,0),B(0,4),请你直接写出所有以格点为顶点,OA、OB 为勾股边且有对角线相等的勾股四边形 OAMB 的顶点M 的坐标: ;
(3)如图 2,将△ABC 绕顶点 B 按顺时针方向旋转 60°,得到△DBE,连接 AD、DC,∠DCB=30°.求证: DC2 BC2 AC2 ,即四边形 ABCD 是勾股四边形;
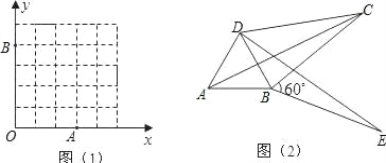
(4)若将图 2 中△ABC 绕顶点 B 按顺时针方向旋转 a 度(0°<a <90°),得到△DBE,连接 AD、DC,则当∠DCB= °时,四边形BECD 是勾股四边形.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:如图,点A,B,C,D的坐标分别是(1,7),(1,1),(4,1),(6,1).若以C,D,E(E在格点上)为顶点的三角形与△ABC相似,则点E的坐标不可能是( )
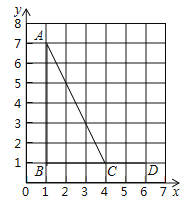
A. (6,0) B. (4,2) C. (6,5) D. (6,3)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】 如图,AB是⊙O的直径,P为AB延长线上的一个动点,过点P作⊙O的切线,切点为C,连接AC,BC,作∠APC的平分线交AC于点D.
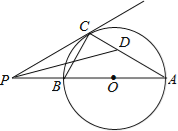
下列结论正确的是 (写出所有正确结论的序号)
①△CPD∽△DPA;
②若∠A=30°,则PC=![]() BC;
BC;
③若∠CPA=30°,则PB=OB;
④无论点P在AB延长线上的位置如何变化,∠CDP为定值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知: A 0,1 , B 2, 0 , C 4, 3 .
(1)求△ABC 的面积;
(2)设点 P 在坐标轴上,且△ABC 和△ABP 的面积相等,直接写出 P 的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知直线l//AB,l与AB之间的距离为2.C、D是直线l上两个动点(点C在D点的左侧),且AB=CD=5.连接AC、BC、BD,将△ABC沿BC折叠得到△A′BC.下列说法:①四边形ABDC的面积始终为10;②当A′与D重合时,四边形ABDC是菱形;③当A′与D不重合时,连接A′、D,则∠CA′D+∠BC A′=180°;④若以A′、C、B、D为顶点的四边形为矩形,则此矩形相邻两边之和为3![]() 或7.其中正确的是( )
或7.其中正确的是( )
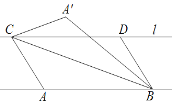
A. ①②③④B. ①③④C. ①②④D. ①②③
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某个体经营户了解到有一种盒装商品能畅销市场,就用4万元购进这种商品,面市后果然供不应求,他又用8.8万元购进了第二批这种商品,所购数量是第一批购进量的2倍,但每盒单价涨了4元,他在销售这种盒装商品时每盒定价都是56元,最后剩下的150盒按八折销售,很快售完,在这两笔生意中,这位个体经营户共赢利多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
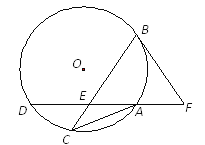
【题目】如图,△ABC内接于⊙O,AB=AC,过点A作AD⊥AB交⊙O于点D,交BC于点E,点F在DA的延长线上,且∠ABF=∠C .
(1)求证:BF是⊙O的切线;
(2)若AD=4,cos∠ABF=![]() ,求BC的长.
,求BC的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,△ABC的三个顶点坐标分别为A(-2,1),B(-1,4),C(-3,2).
(1)画出△ABC关于点B成中心对称的图形△A1BC1;
(2)以原点O为位似中心,相似比为1∶2,在y轴的左侧,画出△ABC放大后的图形△A2B2C2,并直接写出点C2的坐标.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com