Question

4．如图，在平面直角坐标系中，RT△AOB的斜边OB在x轴上，OB=$\frac{50}{3}$，点A在第一象限，∠AOB=90°且OA=10．
（1）求A、B两点的坐标．
（2）在平面内有一点C，使以A、B、O、C为定点的四边形为平行四边形，直接写出点C的坐标；
（3）如图3，P、Q两点同时从A点出发，点P以每秒3个单位的速度沿着AO向O运动，点Q以每秒4个单位的速度沿着AB向B运动（P、Q同时到达终点，且运动过程中PQ始终平行x轴）．设P、Q两点运动时间为t，运动过程中，在x轴是否存在一点M，使以M、P、Q为顶点的三角形为等腰直角三角形，若存在求出t的值；若不存在说明理由．

Answer 1

分析 （1）如图1中，作AE⊥OB于E．先求出AB，再根据$\frac{1}{2}$•OA•AB=$\frac{1}{2}$•OB•AE求出AE，最后利用勾股定理求出OE即可解决问题．
（2）如图2中，点C的位置有三个，写出坐标即可．
（3）分两种情形①当P为等腰直角三角形△PQM的直角顶点时，②当M为等腰直角三角形△PQM的直角顶点时，分别列出方程即可解决问题．

解答 解：（1）如图1中，作AE⊥OB于E．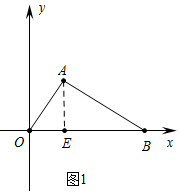

在Rt△AOB中，∵∠OAB=90°，OA=10，OB=$\frac{50}{3}$，
∴AB=$\sqrt{O{B}^{2}-O{A}^{2}}$=$\sqrt{（\frac{50}{3}）^{2}-1{0}^{2}}$=$\frac{40}{3}$，
∵$\frac{1}{2}$•OA•AB=$\frac{1}{2}$•OB•AE，
∴AE=$\frac{OA•AB}{OB}$=8，
∴OE=$\sqrt{O{A}^{2}-A{E}^{2}}$=$\sqrt{1{0}^{2}-{8}^{2}}$=6．
∴A（6，8），B（$\frac{50}{3}$，0）．

（2）如图2中，点C的坐标为（$\frac{32}{3}$，-8）或（$\frac{68}{3}$，8）或（-$\frac{32}{3}$，8）．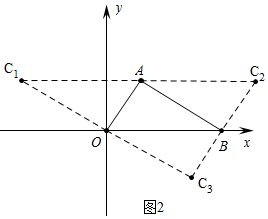


（3）如图3中，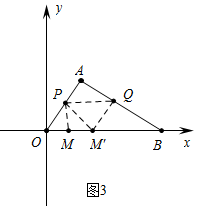

∵AP=3t，AQ=4t，
∴PQ=$\sqrt{A{P}^{2}+A{Q}^{2}}$=5t，OP=10-3t，
∴点P坐标[$\frac{3}{5}$（10-3t），$\frac{4}{5}$（10-3t）]，
①当P为等腰直角三角形△PQM的直角顶点时，PM=PQ，
∴5t=$\frac{4}{5}$（10-3t），
∴t=$\frac{40}{37}$．
②当M为等腰直角三角形△PQM的直角顶点时，有5t=2×$\frac{4}{5}$（10-3t），
∴t=$\frac{80}{49}$．
综上所述，t=$\frac{40}{37}$或$\frac{80}{49}$s时，在x轴是否存在一点M，使以M、P、Q为顶点的三角形为等腰直角三角形．

点评 本题考查四边形综合题、勾股定理、平行四边形的判定和性质、等腰直角三角形的性质等知识，解题的关键是灵活应用这些知识解决问题，学会分类讨论，不能漏解，属于中考压轴题．