
【题目】如图,用正方形是墩垒石梯,下图分别表示垒到一、二阶梯时的情况,那么照这样垒下去
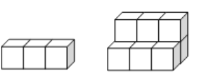
一级 二级
①填出下表中未填的两空,观察规律。
阶梯级数 | 一级 | 二级 | 三级 | 四级 |
石墩块数 | 3 | 9 |
②到第n级阶梯时,共用正方体石墩_______________块(用n的代数式表示)
【答案】①18,30;② ![]()
【解析】
分别数出一、二级台阶中正方体石墩的块数,按照这个规律求得第三、四级台阶中正方体石墩的块数,即可发现第n级台阶中正方体石墩的块数为:![]() .
.
解:①第一级台阶中正方体石墩的块数为:![]() =3;
=3;
第二级台阶中正方体石墩的块数为:3+2×3=3×(1+2)=![]() =9;
=9;
第三级台阶中正方体石墩的块数为:3+2×3+3×3=3×(1+2+3)=![]() =18;
=18;
第四级台阶中正方体石墩的块数为:3+2×3+3×3+3×4=3×(1+2+3+4)= ![]() =30;
=30;
…
依此类推,可以发现:第n级台阶中正方体石墩的块数为:3+2×3+3×3+…+3n=3×(1+2+3+…+n)=![]() .
.
阶梯级数 | 一级 | 二级 | 三级 | 四级 |
石墩块数 | 3 | 9 | 18 | 30 |
故答案为:18,30.
②按照①中总结的规律可得:当垒到第n级阶梯时,共用正方体石墩![]() 块;
块;
故答案为:![]() .
.


科目:初中数学 来源: 题型:
【题目】点D是等边三角形ABC外一点,且DB=DC,∠BDC=120°,将一个三角尺60°角的顶点放在点D上,三角尺的两边DP,DQ分别与射线AB,CA相交于E,F两点.
(1)当EF∥BC时,如图①所示,求证:EF=BE+CF.
(2)当三角尺绕点D旋转到如图②所示的位置时,线段EF,BE,CF之间的上述数量关系是否成立?如果成立,请说明理由;如果不成立,写出EF,BE,CF之间的数量关系,并说明理由.
(3)当三角尺绕点D继续旋转到如图③所示的位置时,(1)中的结论是否发生变化?如果不变化,直接写出结论;如果变化,请直接写出EF,BE,CF之间的数量关系.
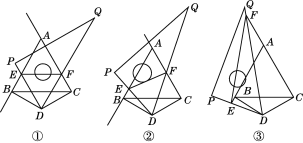
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某食品厂从生产的袋装食品中抽出样品20袋,以每袋标准质量45克为标准,检测每袋的质量是否符合该标准,超过或不足的克数分别用正、负数来表示,记录如下:
与标准质量的差值(单位:克) | ﹣5 | ﹣3 | 0 | 1 | 2 | 5 |
袋数 | 1 | 3 | 6 | 4 | 5 | 1 |
回答下列问题:
(1)这20袋样品中,完全符合每袋标准质量45克的有 袋;
(2)这批样品的总质量是多少克?(要求写出算式).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为了落实党的“精准扶贫”政策,A.,B两城决定向C,D两乡运送肥料以支持农村生产,已知A,B两城共有肥料500吨,其中A城肥料比B城少100吨,从A城往C,D两乡运肥料的费用分别为20元/吨和25元/吨;从B城往C, D两乡运肥料的费用分别为15元/吨和24元/吨。现C乡需要肥料240吨,D乡需要肥料260吨.
(1)A城和B城各有多少吨肥料?
(2)设从A城运往C乡肥料x吨,总运费为y元,求出最少总运费.
(3)由于更换车型,使A城运往C乡的运费每吨减少a(0<a<6)元,这时怎样调运才能使总运费最少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某市举行知识大赛,A校、B校各派出5名选手组成代表队参加决赛,两校派出选手的决赛成绩如图所示.
(1)根据图示填写下表:
平均数/分 | 中位数/分 | 众数/分 | |
A校 | ______ | 85 | ______ |
B校 | 85 | ______ | 100 |
(2)结合两校成绩的平均数和中位数,分析哪个学校的决赛成绩较好;
(3)计算两校决赛成绩的方差,并判断哪个学校代表队选手成绩较为稳定.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,矩形![]() 摆放在平面直角坐标系中,点
摆放在平面直角坐标系中,点![]() 在
在![]() 轴上,点
轴上,点![]() 在
在![]() 轴上,
轴上,![]() ,
,![]() ,过点
,过点![]() 的直线交矩形
的直线交矩形![]() 的边
的边![]() 于点
于点![]() ,且点
,且点![]() 不与点
不与点![]() 、
、![]() 重合,过点
重合,过点![]() 作
作![]() ,
,![]() 交
交![]() 轴于点
轴于点![]() ,交
,交![]() 轴于点
轴于点![]() .
.
(1)若![]() 为等腰直角三角形.
为等腰直角三角形.
①求直线![]() 的函数解析式;
的函数解析式;
②在![]() 轴上另有一点
轴上另有一点![]() 的坐标为
的坐标为![]() ,请在直线
,请在直线![]() 和
和![]() 轴上分别找一点
轴上分别找一点![]() 、
、![]() ,使
,使![]() 的周长最小,并求出此时点
的周长最小,并求出此时点![]() 的坐标和
的坐标和![]() 周长的最小值.
周长的最小值.
(2)如图2,过点![]() 作
作![]() 交
交![]() 轴于点
轴于点![]() ,若以
,若以![]() 、
、![]() 、
、![]() 、
、![]() 为顶点的四边形是平行四边形,求直线
为顶点的四边形是平行四边形,求直线![]() 的解析式.
的解析式.
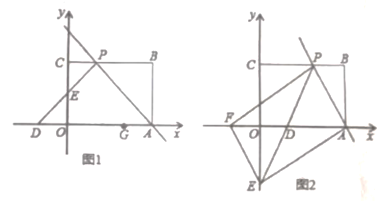
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:二次函数y=ax2+2ax﹣4(a≠0)的图象与x轴交于点A,B(A点在B点的左侧),与y轴交于点C,△ABC的面积为12.
(1)求二次函数图象的对称轴与它的解析式;
(2)点D在y轴上,当以A、O、D为顶点的三角形与△BOC相似时,求点D的坐标;
(3)点D的坐标为(﹣2,1),点P在二次函数图象上,∠ADP为锐角,且tan∠ADP=2,求点P的横坐标.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】小刘对本班同学的业余兴趣爱好进行了一次调查,她根据采集到的数据,绘制了下面的图1和图2.
请你根据图中提供的信息,解答下列问题:
(1)在图1中,将“书画”部分的图形补充完整;
(2)在图2中,求出“球类”部分所对应的圆心角的度数,并分别写出爱好“音乐”、“书画”、“其它”的人数占本班学生数的百分数;
(3)观察图1和图2,你能得出哪些结论(只要写出一条结论).


查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某校有3000名学生.为了解全校学生的上学方式,该校数学兴趣小组以问卷调查的形式,随机调查了该校部分学生的主要上学方式(参与问卷调查的学生只能从以下六个种类中选择一类),并将调查结果绘制成如下不完整的统计图.
种类 | A | B | C | D | E | F |
上学方式 | 电动车 | 私家车 | 公共交通 | 自行车 | 步行 | 其他 |
某校部分学生主要上学方式扇形统计图某校部分学生主要上学方式条形统计图

根据以上信息,回答下列问题:
(1)参与本次问卷调查的学生共有____人,其中选择B类的人数有____人.
(2)在扇形统计图中,求E类对应的扇形圆心角α的度数,并补全条形统计图.
(3)若将A、C、D、E这四类上学方式视为“绿色出行”,请估计该校每天“绿色出行”的学生人数.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com