
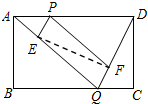
 如图所示,已知矩形ABCD的边长AB=2,BC=3,点P是AD边上的一动点(P不同于A、D),Q是BC边上的任意一点,连接AQ、DQ,过P作PE∥DQ交AQ于E,作PF∥AQ交DQ于F.设AP的长为x,则△PEF的面积y关于x的函数关系式是( )
如图所示,已知矩形ABCD的边长AB=2,BC=3,点P是AD边上的一动点(P不同于A、D),Q是BC边上的任意一点,连接AQ、DQ,过P作PE∥DQ交AQ于E,作PF∥AQ交DQ于F.设AP的长为x,则△PEF的面积y关于x的函数关系式是( )| A. | y=-$\frac{1}{3}$x2+x | B. | y=-$\frac{2}{3}$x2+2x | C. | y=-$\frac{1}{3}$x2+x+3 | D. | y=-$\frac{2}{3}$x2+2x+6 |
分析 由于PE∥DQ,PF∥AQ,因此四边形PEQF是平行四边形,根据平行四边形的性质可知:S△PEF=$\frac{1}{2}$S平行四边形PEQF,可先求出△AQD的面积,然后根据△AEP与△ADQ相似,用相似比的平方即面积比求出△APE的面积,同理可求出△DPF的面积,进而可求出平行四边形PEQF的面积表达式,也就能得出关于y,x的函数关系式.
解答 解:∵PE∥DQ,PF∥AQ,
∴△APE∽△ADQ,△PDF∽△ADQ,S△PEF=$\frac{1}{2}$S平行四边形PEQF,
∴$\frac{{S}_{△AEP}}{{S}_{△AQD}}$=($\frac{x}{3}$)2,$\frac{{S}_{△DPE}}{{S}_{△ADQ}}$=($\frac{3-x}{3}$)2,
∵S△AQD=$\frac{1}{2}$AD×AB=$\frac{1}{2}$×3×2=3,
得S△PEF=$\frac{1}{2}$S平行四边形PEQF
=$\frac{1}{2}$(S△AQD-S△AEP-S△DFP)
=$\frac{1}{2}$×[3-($\frac{x}{3}$)2×3-($\frac{3-x}{3}$)2×3]
=$\frac{1}{2}$(-$\frac{2}{3}$x2+2x)
=-$\frac{1}{3}$x2+x,
即△PEF的面积y关于x的函数关系式是y=-$\frac{1}{3}$x2+x.
故选:A.
点评 此题考查相似三角形的判定与性质,从实际问题中抽象出二次函数,利用平行得出相似三角形是解决问题的关键.


科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
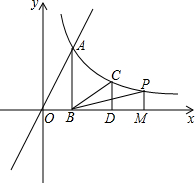 如图,正比例函数y=2x与反比例函数y=$\frac{8}{x}$在第一象限交于点A,过点A作AB⊥x轴于点B.
如图,正比例函数y=2x与反比例函数y=$\frac{8}{x}$在第一象限交于点A,过点A作AB⊥x轴于点B.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 第二、三象限 | B. | 第二、四象限 | C. | 第一、三象限 | D. | 第三、四象限 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
| 上学方式 | 步行 | 骑自行车 | 乘公共汽车 | 其他 |
| 人数 | 30 | 100 | 150 | 20 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com