
【题目】如图,直线![]() 与
与![]() 轴交于
轴交于![]() 点,与反比例函数
点,与反比例函数![]() 的图象交于点
的图象交于点![]() ,过
,过![]() 作
作![]() 轴于点
轴于点![]() ,且
,且![]()
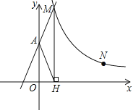
![]() 求
求![]() 的值;
的值;
![]() 点
点![]() 是反比例函
是反比例函![]() 图象上的点,在
图象上的点,在![]() 轴上是否存在点
轴上是否存在点![]() ,使得
,使得![]() 最小?若存在,求出点
最小?若存在,求出点![]() 的坐标;若不存在,请说明理由.
的坐标;若不存在,请说明理由.
【答案】(1)4;(2)存在,点![]() 的坐标为
的坐标为![]() .
.
【解析】
(1)先求出A点坐标,从而得到H的横坐标,即M的横坐标,然后代入直线解析式求得纵坐标,再利用待定系数法求得k的值;
(2)存在,先求出N点的坐标,作![]() 关于
关于![]() 轴的对称点
轴的对称点![]() ,连结
,连结![]() ,交
,交![]() 轴于点
轴于点![]() ,此时
,此时![]() 最小,然后用待定系数法求得直线
最小,然后用待定系数法求得直线![]() 的解析式,再求出其与x轴的交点即可.
的解析式,再求出其与x轴的交点即可.
解:![]() ∵直线
∵直线![]() 与
与![]() 轴交于
轴交于![]() 点,
点,
∴![]() 点坐标为
点坐标为![]() ,
,![]() ,
,
∵![]() ,
,
∴![]() ,
,
∵![]() 轴,
轴,
∴![]() 点横坐标为
点横坐标为![]() ,
,
∵点![]() 在直线
在直线![]() 上,
上,
∴当![]() 时,
时,![]() ,
,
∴![]() ,
,
∵点![]() 在反比例函数
在反比例函数![]() 的图象上,
的图象上,
∴![]() ;
;
![]() 存在.
存在.
∵点![]() 是反比例函
是反比例函![]() 图象上的点,
图象上的点,
∴![]() ,即点
,即点![]() ,
,

作![]() 关于
关于![]() 轴的对称点
轴的对称点![]() ,连结
,连结![]() ,交
,交![]() 轴于点
轴于点![]() ,此时
,此时![]() 最小;
最小;
∵![]() 与
与![]() 关于
关于![]() 轴,点
轴,点![]() ,
,
∴点![]() ,
,
设直线![]() 的解析式为
的解析式为![]() ,
,
则![]() ,解得
,解得 ,
,
∴直线![]() 的解析式为
的解析式为![]() ,
,
令![]() ,得
,得![]() ,
,
∴点![]() 的坐标为
的坐标为![]() .
.


科目:初中数学 来源: 题型:
【题目】金秋十月,丹桂飘香,重庆双福育才中学迎来了首届行知创新科技大赛,初二年级某班共有18人报名参加航海组,航空组和无人机组三个项目组的比赛(每人限参加一项),其中航海组的同学比无人机组的同学的两倍少3人,航空组的同学不少于3人但不超过9人,班级决定为航海组的每位同学购买2个航海模型,为航空组的每位同学购买3个航空模型,为无人机组的每位同学购买若干个无人机模型,已知航海模型75元每个,航空模型98元每个,无人机模型165元每个,若购买这三种模型共需花费6114元,则其中购买无人机模型的费用是__________.
查看答案和解析>>
科目:初中数学 来源: 题型:
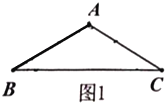
【题目】(问题背景)
(1)如图1,等腰![]() 中,
中,![]() ,
,![]() ,则
,则![]() ______;
______;
(知识应用)
(2)如图2,![]() 和
和![]() 都是等腰三角形,
都是等腰三角形,![]() ,
,![]() 、
、![]() 、
、![]() 三点在同一条直线上,连接
三点在同一条直线上,连接![]() .
.
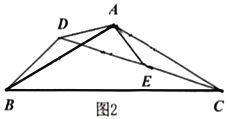
①求证:![]() ;
;
②请写出线段![]() ,
,![]() ,
,![]() 之间的等量关系式,并说明理由?
之间的等量关系式,并说明理由?
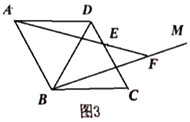
(3)如图3,![]() 和
和![]() 均为等边三角形,在
均为等边三角形,在![]() 内作射线
内作射线![]() ,作点
,作点![]() 关于
关于![]() 的对称点
的对称点![]() ,连接
,连接![]() 并延长交
并延长交![]() 于点
于点![]() ,连接
,连接![]() ,
,![]() .若
.若![]() ,
,![]() ,求
,求![]() 的长.
的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,反比例函数![]() 与一次函数y=x+b的图象,都经过点A(1,2)
与一次函数y=x+b的图象,都经过点A(1,2)

(1)试确定反比例函数和一次函数的解析式;
(2)求一次函数图象与两坐标轴的交点坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某中学为了创建“最美校园图书屋”,新购买了一批图书,其中科普类图书平均每本书的价格是文学类图书平均每本书价格的1.2倍.已知学校用12000元购买文学类图书的本数比用这些钱购买科普类图书的本数多100本,那么学校购买文学类图书平均每本书的价格是多少元?设学校购买文学类图书平均每本书的价格是x元,则下面所列方程中正确的是( )
A. ![]() B.
B. ![]()
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知![]()
![]() ,请用无刻度直尺和圆规,完成下列作图(不要求写作法,保留作图痕迹):
,请用无刻度直尺和圆规,完成下列作图(不要求写作法,保留作图痕迹):
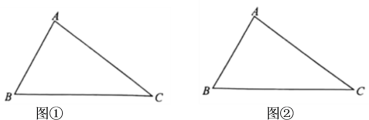
(1)在边![]() 上找一点
上找一点![]() ,使得:将
,使得:将![]() 沿着过点
沿着过点![]() 的某一条直线折叠,点
的某一条直线折叠,点![]() 与点
与点![]() 能重合,请在图①中作出点
能重合,请在图①中作出点![]() ;
;
(2)在边![]() 上找一点
上找一点![]() ,使得:将
,使得:将![]() 沿着过点
沿着过点![]() 的某一条直线折叠,点
的某一条直线折叠,点![]() 能落在边
能落在边![]() 上的点
上的点![]() 处,且
处,且![]() ,请在图②中作出点
,请在图②中作出点![]() .
.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】利用墙为一边,用长为![]() 的材料作另三边,围成一个面积为
的材料作另三边,围成一个面积为![]() 的长方形小花园,这个长方形的长和宽各是( )
的长方形小花园,这个长方形的长和宽各是( )
A. 5m,4m B. 8m,2.5m
C. 10m,2m D. 5m,4m或8m,2.5m
查看答案和解析>>
科目:初中数学 来源: 题型:
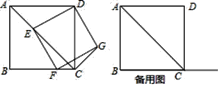
【题目】四边形![]() 为正方形,点
为正方形,点![]() 为线段
为线段![]() 上一点,连接
上一点,连接![]() ,过点
,过点![]() 作
作![]() ,交射线
,交射线![]() 于点
于点![]() ,以
,以![]() 、
、![]() 为邻边作矩形
为邻边作矩形![]() ,连接
,连接![]() .
.
![]() 如图
如图![]() ,求证:矩形
,求证:矩形![]() 是正方形;
是正方形;
![]() 若
若![]() ,
,![]() ,求
,求![]() 的长度;
的长度;
![]() 当线段
当线段![]() 与正方形
与正方形![]() 的某条边的夹角是
的某条边的夹角是![]() 时,直接写出
时,直接写出![]() 的度数.
的度数.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com