阅读材料,解答问题.
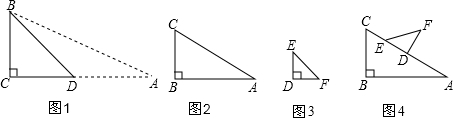
例 如图,在△BCD中,∠C=90°,∠BDC=45°,利用此等腰直角三角形你能求出tan22.5°的值吗?
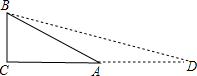
解:延长CD到点A,使AD=BD,连接AB.
设BC=a(a>0).
∵在△BCD中,∠C=90°,∠BDC=45°.
∴∠
A==22.5°.
∴CD=a,
AD=BD=a.
∴
AC=(+1)a.
∴
tan22.5°=====-1.
(1)仿照上例,求出tan15°的值;
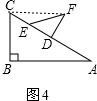
(2)在一次课外活动中,小刘从上例得到启发,用硬纸片做了两个直角三角形,如图1、图2.图1中,∠B=90°,∠A=30°,BC=6cm;图2中,∠D=90°,∠E=45°,DE=4cm.图3是小刘所做的一个实验:他将△DEF的直角边DE与△ABC的斜边AC重合在一起,并将△DEF沿CA方向移动.在移动过程中,D、E两点始终在CA边上(移动开始时点E与点C重合).
①在△DEF沿CA方向移动的过程中,∠FCD的度数逐渐
.(填“不变”、“变大”、“变小”)
②在△DEF移动过程中,是否存在某个位置,使得∠FCD=15°?如果存在,求出AD的长度;如果不存在,请说明理由.