
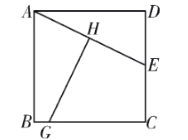
【题目】如图,![]() 是正方形
是正方形![]() 的边
的边![]() 的中点,
的中点,![]() 的垂直平分线分别交
的垂直平分线分别交![]() 、
、![]() 于
于![]() 、
、![]() ,若
,若![]() ,则
,则![]() 的长为__________.
的长为__________.
【答案】![]()
【解析】
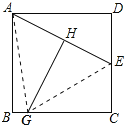
连接AG、EG,设CE=x,则AB=BC=2x,BG=2x-7,根据线段垂直平分线的性质得出AG=EG,根据勾股定理得出方程,解方程即可求出CE,从而得到AD,DE,BG,算出AG,再根据勾股定理可得GH.
解:连接AG、EG,如图所示:
∵四边形ABCD是正方形,
∴AB=BC=CD,
∵E是正方形ABCD的边CD的中点,
∴CE=![]() CD,
CD,
设CE=x,则AB=BC=2x,BG=2x-7,
∵AE的垂直平分线分别交AE、BC于H、G,
∴AG=EG,
在Rt△AGH和Rt△EGH中,
根据勾股定理得:AG2=AB2+BG2,EG2=CE2+CG2,
∴(2x)2+(2x-7)2=x2+72,
解得:x=4,即CE=4=DE,
∴AB=8=AD,BG=1,
∴AE=![]() ,
,
∴AH=![]() ,
,
∵AG=![]() ,
,
∴GH=![]() .
.
故答案为:![]() .
.


科目:初中数学 来源: 题型:
【题目】为了提高身体素质,有些人选择到专业的健身中心锻炼身体,某健身中心的消费方式如下:
普通消费:35元/次;
白金卡消费:购卡280元/张,凭卡免费消费10次再送2次;
钻石卡消费:购卡560元/张,凭卡每次消费不再收费.
以上消费卡使用年限均为一年,每位顾客只能购买一张卡,且只限本人使用.
(1)李叔叔每年去该健身中心健身6次,他应选择哪种消费方式更合算?
(2)设一年内去该健身中心健身x次(x为正整数),所需总费用为y元,请分别写出选择普通消费和白金卡消费的y与x的函数关系式;
(3)王阿姨每年去该健身中心健身至少18次,请通过计算帮助王阿姨选择最合算的消费方式.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】定义:若![]() ,则称
,则称![]() 与
与![]() 是关于
是关于![]() 的关联数.例如:若
的关联数.例如:若![]() ,则称
,则称![]() 与
与![]() 是关于2的关联数;
是关于2的关联数;
(1)若3与![]() 是关于5的关联数,求
是关于5的关联数,求![]() 的值
的值
(2)若![]() 与
与![]() 是关于4的关联数,求
是关于4的关联数,求![]() 的值.
的值.
(3)若![]() 与
与![]() 是关于
是关于![]() 的关联数,
的关联数, ![]() ,
,![]() 的值与
的值与![]() 无关,求
无关,求![]() 的值.
的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,一次函数y=mx+n(m≠0)的图象与反比例函数![]() (k≠0)的图象交于第一、三象限内的A、B两点,与y轴交于点C,过点B作BM⊥x轴,垂足为M,BM=OM,OB=
(k≠0)的图象交于第一、三象限内的A、B两点,与y轴交于点C,过点B作BM⊥x轴,垂足为M,BM=OM,OB=![]() ,点A的纵坐标为4.
,点A的纵坐标为4.
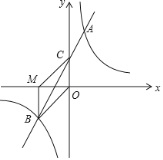
(1)求该反比例函数和一次函数的解析式;
(2)连接AO,求△AOB的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,在![]() 中,弦
中,弦![]() 弦
弦![]() ,垂足为点
,垂足为点![]() ,连接
,连接![]() 、
、![]() 、
、![]() ,
,![]() .
.
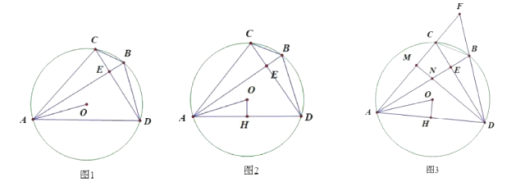
(1)求证:![]()
(2)如图2,过点![]() 作
作![]() ,垂足为点
,垂足为点![]() ,求证:
,求证:![]()
(3)如图3,在(2)的条件下,延长![]() 、
、![]() 交于点
交于点![]() ,过点
,过点![]() 作
作![]() ,垂足为
,垂足为![]() ,交
,交![]() 于
于![]() ,若
,若![]() ,
,![]() ,求
,求![]() 的长.
的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】小方与小辉在玩军棋游戏,他们定义了一种新的规则,用军棋中的“工兵”、“连长”、“地雷”比较大小,共有6个棋子,分别为1个“工兵”,2个“连长”,3个“地雷”游戏规则如下:①游戏时,将棋反面朝上,两人随机各摸一个棋子进行比赛,先摸者摸出的棋不放回;②“工兵”胜“地雷”,“地雷”胜“连长”,“连长”胜“工兵”;③相同棋子不分胜负.
(1)若小方先摸,则小方摸到“排长”的事件是 ;若小方先摸到了“连长”,小辉在剩余的5个棋子中随机摸一个,则这一轮中小方胜小辉的概率为 .
(2)如果先拿走一个“连长”,在剩余的5个棋子中小方先摸一个棋子,然后小辉在剩余的4个棋子中随机摸一个,求这一轮中小方获胜的概率 .

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,CD是⊙O的弦,AB是直径,且CD∥AB,连接AC、AD、OD,其中AC=CD,过点B的切线交CD的延长线于E.
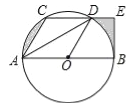
(1)求证:DA平分∠CDO;
(2)若AB=12,求图中阴影部分的周长之和(参考数据:π=3.1,![]() =1.4,
=1.4,![]() =1.7).
=1.7).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】一个不透明的口袋中装有4个分别标有数1,2,3,4的小球,它们的形状、大小完全相同,小红先从口袋里随机摸出一个小球记下数为x,小颖在剩下的3个球中随机摸出一个小球记下数为y,这样确定了点P(x,y),请用“列表法”或“树状图法”求点P(x,y)在函数y=-x+5图象上的概率.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com