
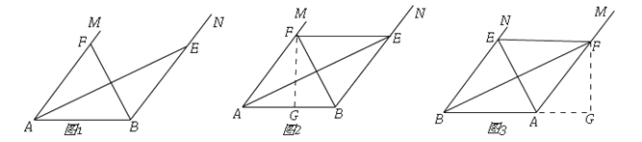
【题目】在线段AB的同侧作射线AM和BN,若∠MAB与∠NBA的平分线分别交射线BN,AM于点E,F,AE和BF交于点P.如图,点点同学发现当射线AM,BN交于点C;且∠ACB=60°时,有以下两个结论:
①∠APB=120°;②AF+BE=AB.
那么,当AM∥BN时:
(1)点点发现的结论还成立吗?若成立,请给予证明;若不成立,请求出∠APB的度数,写出AF,BE,AB长度之间的等量关系,并给予证明;
(2)设点Q为线段AE上一点,QB=5,若AF+BE=16,四边形ABEF的面积为![]() ,求AQ的长.
,求AQ的长.

【答案】(1)原命题不成立,新结论为:∠APB=90°,AF+BE=2AB(或AF=BE=AB);(2)当∠FAB=60°时,AQ=![]() 或
或![]() .
.
【解析】
试题分析:(1)由角平分线和平行线整体求出∠MAB+∠NBA,从而得到∠APB=90°,最后用等边对等角,即可.
(2)先根据条件求出AF,FG,求出∠FAG=60°,最后分两种情况讨论计算.
试题解析:(1)原命题不成立,新结论为:∠APB=90°,AF+BE=2AB(或AF=BE=AB).
理由:∵AM∥BN,∴∠MAB+∠NBA=180°,∵AE,BF分别平分∠MAB,NBA,∴∠EAB=![]() ∠MAB,∠FBA=
∠MAB,∠FBA=![]() ∠NBA,∴∠EAB+∠FBA=
∠NBA,∴∠EAB+∠FBA=![]() (∠MAB+∠NBA)=90°,∴∠APB=90°,∵AE平分∠MAB,∴∠MAE=∠BAE,∵AM∥BN,∴∠MAE=∠BAE,∴∠BAE=∠BEA,∴AB=BE,同理:AF=AB,∴AF=+BE=2AB(或AF=BE=AB);
(∠MAB+∠NBA)=90°,∴∠APB=90°,∵AE平分∠MAB,∴∠MAE=∠BAE,∵AM∥BN,∴∠MAE=∠BAE,∴∠BAE=∠BEA,∴AB=BE,同理:AF=AB,∴AF=+BE=2AB(或AF=BE=AB);
(2)如图1,过点F作FG⊥AB于G,∵AF=BE,AF∥BE,∴四边形ABEF是平行四边形,∵AF+BE=16,∴AB=AF=BE=8,∵![]() =8×FG,∴FG=
=8×FG,∴FG=![]() ,在Rt△FAG中,AF=8,∴∠FAG=60°,当点G在线段AB上时,∠FAB=60°,当点G在线段BA延长线时,∠FAB=120°.
,在Rt△FAG中,AF=8,∴∠FAG=60°,当点G在线段AB上时,∠FAB=60°,当点G在线段BA延长线时,∠FAB=120°.
①如图2,当∠FAB=60°时,∠PAB=30°,∴PB=4,PA=![]() ,∵BQ=5,∠BPA=90°,∴PQ=3,∴AQ=
,∵BQ=5,∠BPA=90°,∴PQ=3,∴AQ=![]() 或AQ=
或AQ=![]() .
.
②如图3,当∠FAB=120°时,∠PAB=60°,∠FBG=30°,∴PB=![]() ,∵PB=
,∵PB=![]() >5,∴线段AE上不存在符合条件的点Q,∴当∠FAB=60°时,AQ=
>5,∴线段AE上不存在符合条件的点Q,∴当∠FAB=60°时,AQ=![]() 或
或![]() .
.


 应用题天天练四川大学出版社系列答案
应用题天天练四川大学出版社系列答案科目:初中数学 来源: 题型:
【题目】如图:
(1)如果∠1=∠4,根据 , 可得AB∥CD;
(2)如果∠1=∠2,根据 , 可得AB∥CD;
(3)如果∠1+∠3=180,根据 , 可得AB∥CD .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为了参加中学生篮球运动会,一支篮球队准备购买10双运动鞋,各种尺码统计如下表:
尺码(厘米) | 40 | 40.5 | 41 | 41.5 | 42 |
购买量(双) | 1 | 2 | 3 | 2 | 2 |
则这10双运动鞋尺码的众数和中位数分别为( )
A. 40.5;41 B. 41;41 C. 40.5;40.5 D. 41;40.5
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图所示,已知O是∠APB内的一点,点M、N分别是O点关于PA、PB的对称点,MN与PA、PB分别相交于点E、F,已知MN=5cm,求△OEF的周长。
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】设直线l1和直线l2平行,且l1和l2间的距离为a.如果线段AB在l1的右侧,并设AB关于l1的对称图形是A′B′,而A′B′关于l2的对称图形是A″B″(如图),那么,线段AB和A″B″有什么关系?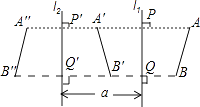
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知点A(﹣1,y1),点B(2,y2)在抛物线y=﹣3x2+2上,则y1,y2的大小关系是( )
A.y1>y2B.y1<y2C.y1=y2D.无法判断
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com