
| A. | y=x2+x-3 | B. | y=2(x-1)2-3 | C. | y=$\frac{1}{2}$(x-1)(x+1) | D. | y=3x2-3 |
分析 根据题意列出a与b的方程组,求出方程组的解得到a与b的值,确定出解析式,然后根据顶点的变化确定出可以平移得到的函数解析式即可得解.
解答 解:根据题意得:$\left\{\begin{array}{l}{-\frac{b}{2a}=1}\\{a-b-3=0}\end{array}\right.$,
解得:a=1,b=-2,
则函数解析式为y=x2-2x-3=(x-1)2-4,
所以抛物线y=x2-2x-3向左平移$\frac{1}{2}$个单位,向下平移$\frac{1}{2}$个单位得到y=x2+x-3,
故选A.
点评 本题考查了待定系数法求二次函数的解析式以及二次函数图象与几何变换,此类题目利用顶点的变化确定函数解析式的变化是解题的关键,平移的规律:左加右减,上加下减.


 一诺书业暑假作业快乐假期云南美术出版社系列答案
一诺书业暑假作业快乐假期云南美术出版社系列答案科目:初中数学 来源: 题型:选择题
| A. | n2+n | B. | n2+n+1 | C. | n2+2n | D. | n2+2n+1 |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
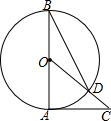 如图,AB是⊙O的直径,AC是⊙O的切线,连接OC与⊙O相交于点D,连接BD,∠C=40°,若点P为优弧$\widehat{ABD}$上的动点,连接PA、PD,则∠APD的大小是25度.
如图,AB是⊙O的直径,AC是⊙O的切线,连接OC与⊙O相交于点D,连接BD,∠C=40°,若点P为优弧$\widehat{ABD}$上的动点,连接PA、PD,则∠APD的大小是25度.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 正方形ABCD,点E在AD上,点F为CE的中点,过点F作CE的垂线交AB,CD于点H,G.
正方形ABCD,点E在AD上,点F为CE的中点,过点F作CE的垂线交AB,CD于点H,G.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
 如图,在等边△ABC中,点D在BC上,且BD=$\frac{1}{2}$CD,点E在AB上,点F在AC上,∠EDF=120°.若BE=2CF,且四边形AEDF的面积为$\frac{37\sqrt{3}}{4}$,则EF的长为$\frac{7\sqrt{15}}{5}$.
如图,在等边△ABC中,点D在BC上,且BD=$\frac{1}{2}$CD,点E在AB上,点F在AC上,∠EDF=120°.若BE=2CF,且四边形AEDF的面积为$\frac{37\sqrt{3}}{4}$,则EF的长为$\frac{7\sqrt{15}}{5}$.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
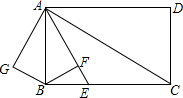 如图在矩形ABCD中,AB=6,AD=8,AE平分∠BAC交BC于点E,过B作BF⊥AE交AE于点F,将△ABF沿AB翻折得到△ABG,将△ABG绕点A逆时针旋转角a,(其中0°<a<180°)记旋转中的△ABG为△AB′G′,在旋转过程中,设直线B′G′分别与直线AD、直线AC交于点M、N,当MA=MN时,线段MD长为8-$\frac{5\sqrt{5}}{2}$.
如图在矩形ABCD中,AB=6,AD=8,AE平分∠BAC交BC于点E,过B作BF⊥AE交AE于点F,将△ABF沿AB翻折得到△ABG,将△ABG绕点A逆时针旋转角a,(其中0°<a<180°)记旋转中的△ABG为△AB′G′,在旋转过程中,设直线B′G′分别与直线AD、直线AC交于点M、N,当MA=MN时,线段MD长为8-$\frac{5\sqrt{5}}{2}$.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
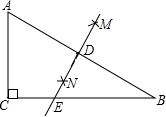 如图,在△ABC中,∠ACB=90°,分别以点A和点B为圆心,以相同的长(大于$\frac{1}{2}$AB)为半径作弧,两弧相交于点M和点N,作直线MN交AB于点D,交BC于点E.若AC=3,AB=5,则DE等于( )
如图,在△ABC中,∠ACB=90°,分别以点A和点B为圆心,以相同的长(大于$\frac{1}{2}$AB)为半径作弧,两弧相交于点M和点N,作直线MN交AB于点D,交BC于点E.若AC=3,AB=5,则DE等于( )| A. | 2 | B. | $\frac{10}{3}$ | C. | $\frac{15}{8}$ | D. | $\frac{15}{2}$ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com