值得探究的“叠放”！
问题提出：把八个一样大小的正方体（棱长为1）叠放在一起，形成一个长方体（或正方体），这样的长方体（或正方体）表面积最小是多少？
方法探究：
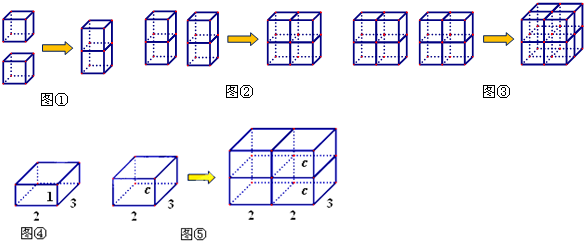
第一步，取两个正方体叠放成一个长方体（如图①），由此可知，新长方体的长、宽、高分别为1，1，2．
第二步，将新长方体看成一个整体，六个面中面积最大的是2，取相同的长方体，紧挨最大面积的面进行“叠放”，可形成一个较大的长方体（如图②），该长方体的长、宽、高分别为2，1，2．
第三步，将较大的长方体看成一个整体，六个面中面积最大的是4，取相同的长方体，紧挨最大面积的面进行“叠放”，可形成一个大的正方体（如图③），该正方体的长、宽、高分别为2，2，2．
这样，八个大小一样的正方体所叠放成的大正方体的最小表面积为6×2×2=24．
仔细阅读上述文字，利用其中思想方法解决下列问题：
（1）如图④，长方体的长、宽、高分别为2，3，1，请计算这个长方体的表面积．提示：长方体的表面积=2×（长×宽+宽×高+长×高）
（2）取如图④的长方体四个进行叠放，形成一个新的长方体，那么，新的长方体的表面积最小是多少？
（3）取四个长、宽、高分别为2，3，c的长方体进行叠放如图⑤，此时，形成一个新的长方体表面积最小，求c的取值范围．
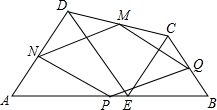如图，在四边形ABCD中，E为AB上一点，△ADE和△BCE都是等边三角形，AB、BC、CD、DA的中点分别为P、Q、M、N，
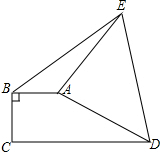如图，直角梯形ABCD中，AB∥CD，AB⊥BC，AB=2，将腰DA以A为旋转中心逆时针旋转90°至AE，连接BE，DE，△ABE的面积为3，则CD的长为
如图，在△ABC中，AB=AC，D、E分别是AC，AB上的点，且BD=BC，BE=ED=AD，求∠A的度数．