
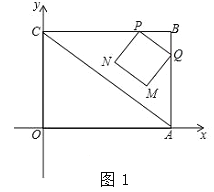
【题目】已知矩形OABC在如图所示平面直角坐标系中,点B的坐标为(4,3),连接AC.动点P从点B出发,以2cm/s的速度,沿直线BC方向运动,运动到C为止(不包括端点B、C),过点P作PQ∥AC交线段BA于点Q,以PQ为边向下作正方形PQMN,设正方形PQMN与△ABC重叠部分图形面积为S(cm2),设点P的运动时间为t(s).
(1)请用含t的代数式表示BQ长和N点的坐标;
(2)求S与t之间的函数关系式,并指出t的取值范围;
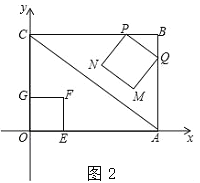
(3)如图2,点G在边OC上,且OG=1cm,在点P从点B出发的同时,另有一动点E从点O出发,以2cm/s的速度,沿x轴正方向运动,以OG、OE为一组邻边作矩形OEFG.试求当点F落在正方形PQMN的内部(不含边界)时t的取值范围.
【答案】(1)![]() ;(2)
;(2) ;(3)
;(3)![]()
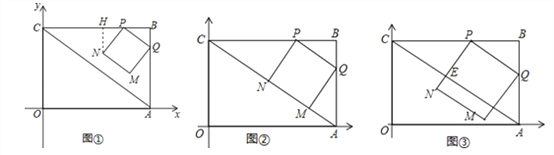
【解析】试题分析:(1)作NH⊥BC于点H,根据△BPQ∽△BCA,利用相似三角形的对应边的比相等求得BQ,然后证明△BPQ≌△HNP,则BH以及HN的长即可利用t表示,则N的坐标即可求解;
(2)首先求出MN在AC上时t的值,然后分两种情况进行讨论,利用矩形的面积公式即可求解;
(3)求得AC的解析式,然后根据PQ∥AC,MN∥AC即可求得PQ和MN的解析式,F的坐标是(2t,1),把F的坐标分别代入PQ和MN的解析式即可求解
试题解析:解:(1)作NH⊥BC于点H.
∵PQ∥CA,∴△BPQ∽△BCA,∴![]() ,即
,即![]() ,解得:BQ=
,解得:BQ=![]() t.∵在△BPQ和△HNP,∴
t.∵在△BPQ和△HNP,∴ ,∴△BPQ≌△HNP,∴HP=BQ=
,∴△BPQ≌△HNP,∴HP=BQ=![]() t,NH=BP=2t,则BH=2t+
t,NH=BP=2t,则BH=2t+![]() t=
t=![]() t,则N点坐标(4﹣
t,则N点坐标(4﹣![]() t,3﹣2t);
t,3﹣2t);
(2)当MN在AC上时,如图②.
∵△BPQ∽△BCA,∴![]() ,即
,即![]() ,解得:PQ=
,解得:PQ=![]() t,当MN在AC上时,PN=PQ=
t,当MN在AC上时,PN=PQ=![]() t,△ABC∽△PNC,即
t,△ABC∽△PNC,即![]() ,即
,即![]() ,解得:t=
,解得:t=![]() .
.
则S=![]() t2.其中,0<t≤
t2.其中,0<t≤![]() .
.
当t>![]() 时,设PN交AC于点E,如图③.
时,设PN交AC于点E,如图③.
则△ABC∽△PEC,则![]() ,即
,即![]() ,解得:PE=
,解得:PE=![]() ,则S=﹣3t2+6t.其中,
,则S=﹣3t2+6t.其中,![]() <t<2.
<t<2.
综上所述:S= ;
;
(3)设AC的解析式是y=kx+b,则![]() ,解得:
,解得: ,则设直线MN的解析式是y=﹣
,则设直线MN的解析式是y=﹣![]() x+3,则﹣
x+3,则﹣![]() (4﹣
(4﹣![]() t)+c=3﹣2t,解得:c=6﹣
t)+c=3﹣2t,解得:c=6﹣![]() t,则直线的解析式是y=﹣
t,则直线的解析式是y=﹣![]() x+(6﹣
x+(6﹣![]() t).
t).
同理,直线PQ的解析式是y=﹣![]() x+(
x+(![]() ﹣
﹣![]() t),F的坐标是(2t,1).
t),F的坐标是(2t,1).
当点F落在MN上时,t=![]() .
.
当点F落在PQ上时,∴t=![]() <t<
<t<![]() .
.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
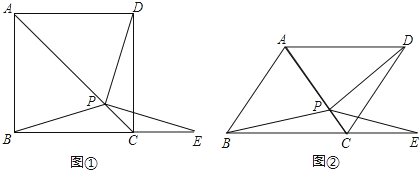
【题目】如图①,在正方形ABCD中,P是对角线AC上的一点,点E在BC的延长线上,且PE=PB.
(1)求证:△BCP≌△DCP;
(2)求证:∠DPE=∠ABC;
(3)把正方形ABCD改为菱形,其它条件不变(如图②),若∠ABC=58°,则∠DPE= 度.
查看答案和解析>>
科目:初中数学 来源: 题型:
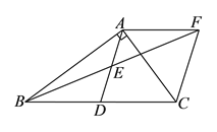
【题目】如图,在Rt△ABC中,BAC 90o,D是BC的中点,E是AD的中点,过点A作AF//BC 交 BE的延长线于点F,连接CF.
(1)求证:AD=AF.
(2)当AB=AC=![]() 时,求四边形ADCF 的面积.
时,求四边形ADCF 的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,菱形ABCD的对角线AC,BD相交于点O,∠ABC=60°,过点B作AC的平行线交DC的延长线于点E.
(1) 求证:四边形ABEC为菱形;
(2) 若AB=6,连接OE,求OE的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】先观察下列各式,再解答后面问题:
![]() =x2+11x+30;
=x2+11x+30;![]() =x2﹣11x+30;
=x2﹣11x+30;
![]() =x2+x﹣30;
=x2+x﹣30;![]() =x2﹣x﹣30;
=x2﹣x﹣30;
(1)根据以上各式呈现的规律,用公式表示出来,则![]() = ;
= ;
(2)试用你写的公式,直接写出下列两式的结果
①![]() = ;
= ;
②![]() = .
= .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,海中有一小岛P,在距小岛P的![]() 海里范围内有暗礁,一轮船自西向东航行,它在A处时测得小岛P位于北偏东60°,且A、P之间的距离为32海里,若轮船继续向正东方向航行,轮船有无触礁危险?请通过计算加以说明.如果有危险,轮船自A处开始至少沿东偏南多少度方向航行,才能安全通过这一海域?
海里范围内有暗礁,一轮船自西向东航行,它在A处时测得小岛P位于北偏东60°,且A、P之间的距离为32海里,若轮船继续向正东方向航行,轮船有无触礁危险?请通过计算加以说明.如果有危险,轮船自A处开始至少沿东偏南多少度方向航行,才能安全通过这一海域?

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】“二广”高速在益阳境内的建设正在紧张地进行,现有大量的沙石需要运输.“益安”车队有载重量为8吨、10吨的卡车共12辆,全部车辆运输一次能运输110吨沙石.
(1)求“益安”车队载重量为8吨、10吨的卡车各有多少辆?
(2)随着工程的进展,“益安”车队需要一次运输沙石165吨以上,为了完成任务,准备新增购这两种卡车共6辆,车队有多少种购买方案,请你一一写出.
查看答案和解析>>
科目:初中数学 来源: 题型:
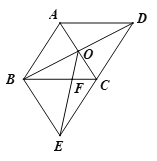
【题目】正方形ABCD和正方形CEFG如图1所示,其中B、C、E在一条直线上,O是AF的中点,连接OD、OG
(1)探究OD与OG的位置关系![]() 的值;(写出结论不用证明)
的值;(写出结论不用证明)
(2)如图2所示,将正方形ABCD和正方形CEFG改为菱形ABCD和菱形CEFG,且∠ABC=∠DCE=120°,探究OD与OG的位置关系,及![]() 的比值;
的比值;
(3)拓展探索:把图1中的正方形CEFG绕C顺时针旋转小于90°的角后,其他条件均不变,问第1问中的两个结论是否发生变化?(写出结论不用证明)

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com