
如图,在平面直角坐标系中,直线y=2x+b(b<0)与坐标轴交于A,B两点,与双曲线y=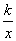 (x>0)交于D点,过点D作DC⊥x轴于点C,连接OD.已知△AOB≌△ACD. www-2-1-cnjy-com
(x>0)交于D点,过点D作DC⊥x轴于点C,连接OD.已知△AOB≌△ACD. www-2-1-cnjy-com
(1)若b=﹣2,求双曲线的解析式;
(2)试探究k与b的数量关系,并写出直线OD的解析式.
 金钥匙试卷系列答案
金钥匙试卷系列答案科目:初中数学 来源: 题型:
情境观察
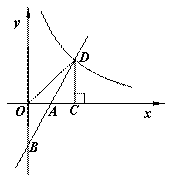
将矩形ABCD纸片沿对角线AC剪开,得到△ABC和△A′C′D,如图1所示.将△A′C′D的顶点A′与点A重合,并绕点A按逆时针方向旋转,使点D、A(A′)、B在同一条直线上,如图2所示.
观察图2可知:与BC相等的线段是 ,∠CAC′= °.
问题探究
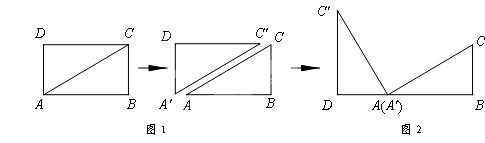
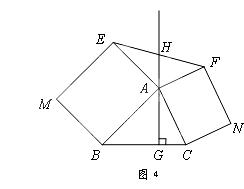
如图3,△ABC中,AG⊥BC于点G,以A为直角顶点,分别以AB、AC为直角边,向△ABC外作等腰Rt△ABE和等腰Rt△ACF,过点E、F作射线GA的垂线,垂足分别为P、Q. 试探究EP与FQ之间的数量关系,并证明你的结论.
拓展延伸
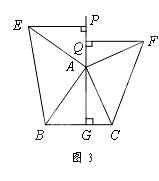
如图4,△ABC中,AG⊥BC于点G,分别以AB、AC为一边向△ABC外作矩形ABME和矩形ACNF,射线GA交EF于点H. 若AB= k AE,AC= k AF,试探究HE与 HF之间的数量关系,并说明理由.
HF之间的数量关系,并说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
如图,△ACE是以□ABCD的对角线AC为边的等边三角形,点C与点E关于x轴对称.若E点的坐标是(7,﹣3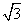 ),则D点的坐标为…………………………………【 】
),则D点的坐标为…………………………………【 】
A.(3,0) B.(4,0) C.(5,0) D.(6,0)

查看答案和解析>>
科目:初中数学 来源: 题型:
观察分析下列方程:①x+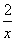 =3;②x+
=3;②x+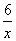 =5;③
=5;③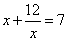 ;请利用它们所蕴含的规律,求关于x的方程x+
;请利用它们所蕴含的规律,求关于x的方程x+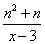 =2n+4(n为正整数)的根,你的答案是__________________
=2n+4(n为正整数)的根,你的答案是__________________
查看答案和解析>>
科目:初中数学 来源: 题型:
某超市销售多种颜色的服装,其中平均每天销售红、黄、蓝、白4种颜色运动服的数量如下表,由此绘制的不完整的扇形统计图如下图.2-1-c-n-j-y
| 服装颜色 | 红 | 黄 | 蓝 | 白 | 合计 |
| 数量/件 | 20 | n | 40 | 1.5n | m |
| 所对扇形的圆心角 |
| 90° | 360° |

(1)求表中m,n,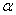 的值,并将扇形统计图补充完整;
的值,并将扇形统计图补充完整;
(2)为吸引更多的顾客,超市将上述扇形统计图制成一个可自由转动的转盘,并规定:顾客在本超市购买商品金额达到一定的数目,就获得一次转动转盘的机会.如果转盘停止后,指针指向红色服装区域、黄色服装区域,可分别获得60元、20元的购物券,求顾客每转动一次转盘获得购物券金额的平均数.
查看答案和解析>>
科目:初中数学 来源: 题型:
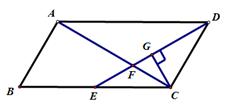
如图, ABCD中,AB=3cm,AD=6cm,∠ADC的角平分线DE交BC于点E,交AC于点F,CG⊥DE,垂足为G,DG=
ABCD中,AB=3cm,AD=6cm,∠ADC的角平分线DE交BC于点E,交AC于点F,CG⊥DE,垂足为G,DG=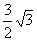 cm,则EF的长为
cm,则EF的长为
A.2cm B.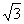 cm C.1cm D.
cm C.1cm D.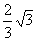 cm
cm
查看答案和解析>>
科目:初中数学 来源: 题型:
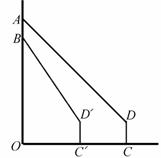
“五一”假期间,小华到小明家邀请小明到新华书店看书,当小华到达CD(点D是小华的眼睛)处时,发现小明在七楼 处,此时测得仰角为45°,继
处,此时测得仰角为45°,继 续向前走了10m到达
续向前走了10m到达 处,发现小明在六楼B处,此时测得仰角为
处,发现小明在六楼B处,此时测得仰角为 ,已知楼层高AB=3m,求O
,已知楼层高AB=3m,求O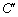 的长. (结果保留根号)
的长. (结果保留根号)
 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com