
分析 (1)利用配方法得到(x-2)2=3,然后利用直接开平方法解方程;
(2)先变形得到3x(x-1)+2(x-1)=0,然后利用因式分解法解方程;
(3)先把方程化为一般式,然后利用因式分解法解方程;
(4)利用求根公式法解方程.
解答 解:(1)x2-4x=-1,
x2-4x+4=-1+4,
(x-2)2=3,
x-2=$±\sqrt{3}$
所以x1=$2+\sqrt{3}$,x2=$2-\sqrt{3}$;
(2)3x(x-1)=2(1-x),
3x(x-1)+2(x-1)=0
(x-1)(3x+2)=0,
x-1=0或3x+2=0,
所以x1=1; x2=-$\frac{3}{2}$;
(3)x2-5x+6=12,
x2-5x-6=0,
(x-6)(x+1)=0,
所以x1=6; x2=-1,
(4)解方程:2x2-2$\sqrt{2}$x-5=0;
x=$\frac{2\sqrt{2}±\sqrt{8-4×2×(-5)}}{4}$ …(2分)
所以x1=$\frac{\sqrt{2}+2\sqrt{3}}{2}$; x2=$\frac{\sqrt{2}-2\sqrt{3}}{2}$.
点评 本题考查了解一元二次方程-因式分解法:先把方程的右边化为0,再把左边通过因式分解化为两个一次因式的积的形式,那么这两个因式的值就都有可能为0,这就能得到两个一元一次方程的解,这样也就把原方程进行了降次,把解一元二次方程转化为解一元一次方程的问题了(数学转化思想).也考查了配方法和公式法解一元二次方程.


 备战中考寒假系列答案
备战中考寒假系列答案科目:初中数学 来源: 题型:解答题
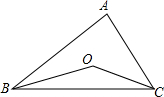 如图,在△ABC中,∠ABC、∠ACB的平分线交于O点.
如图,在△ABC中,∠ABC、∠ACB的平分线交于O点.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
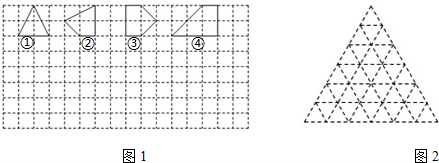
| 多边形的序号 | ① | ② | ③ | ④ | … |
| 多边形的面积S | 2 | 2.5 | 3 | 4 | … |
| 各边上格点的个数和x | 4 | 5 | 6 | 8 | … |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
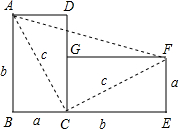 如图,将边长为a与b、对角线长为c的长方形纸片ABCD,绕点C顺时针旋转90°得到长方形FGCE,连接AF.通过用不同方法计算梯形ABEF的面积可验证一条我们学过的定理,该定理的名称是勾股定理,请你写出验证的过程.
如图,将边长为a与b、对角线长为c的长方形纸片ABCD,绕点C顺时针旋转90°得到长方形FGCE,连接AF.通过用不同方法计算梯形ABEF的面积可验证一条我们学过的定理,该定理的名称是勾股定理,请你写出验证的过程.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com