
【题目】(阅读材料)
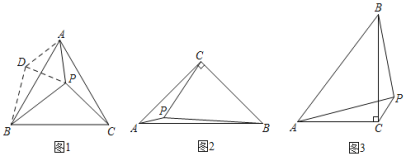
小明遇到这样一个问题:如图1,点P在等边三角形ABC内,且∠APC=150°,PA=3,PC=4,求PB的长.
小明发现,以AP为边作等边三角形APD,连接BD,得到△ABD;由等边三角形的性质,可证△ACP≌△ABD,得PC=BD;由已知∠APC=150°,可知∠PDB的大小,进而可求得PB的长.
(1)请回答:在图1中,∠PDB= °,PB= .
(问题解决)
(2)参考小明思考问题的方法,解决下面问题:
如图2,△ABC中,∠ACB=90°,AC=BC,点P在△ABC内,且PA=1,PB=![]() ,PC=
,PC=![]() ,求AB的长.
,求AB的长.
(灵活运用)
(3)如图3,在Rt△ABC中,∠ACB=90°,∠BAC=α,且tanα=![]() ,点P在△ABC外,且PB=3,PC=1,直接写出PA长的最大值.
,点P在△ABC外,且PB=3,PC=1,直接写出PA长的最大值.
【答案】(1)90°,5;(2)![]() ;(3)
;(3)![]() .
.
【解析】
(1)由△ACP≌△ABD,得∠ADB=∠APC=150°,PC=BD=4,AD=AP=3,因为△ADP为等边三角形,所以∠ADP=60°,DP=AD=3,可得∠BDP=90°,在Rt△BDP中,用勾股定理可求得PB的长;
(2)如图2中,把△ACP绕点C逆时针旋转90°得到△BCD.首先证明∠PDB=90°,再证明A,P,D共线,利用勾股定理即可解决问题.
(3)如图3中,作CD⊥CP,使得CD=![]() PC=
PC=![]() ,则PD=
,则PD=![]() ,利用相似三角形的性质求出AD,即可解决问题.
,利用相似三角形的性质求出AD,即可解决问题.
(1)如图1中,
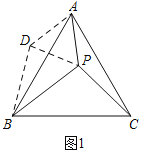
∵△ACP≌△ABD,
∴∠PDB=∠APC=150°,PC=BD=4,AD=AP=3,
∵△ADP为等边三角形,
∴∠ADP=60°,DP=AD=3,
∴∠BDP=150°﹣60°=90°,
∴PB=![]() =5.
=5.
(2)如图2中,把△ACP绕点C逆时针旋转90°得到△BCD.
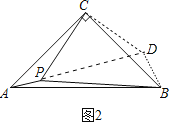
由旋转性质可知;BD=PA=1,CD=CP=2![]() ,∠PCD=90°,
,∠PCD=90°,
∴△PCD是等腰直角三角形,
∴PD=![]() PC=
PC=![]() ×2
×2![]() =4,∠CDP=45°,
=4,∠CDP=45°,
∵PD2+BD2=42+12=17,PB2=(![]() )2=17,
)2=17,
∴PD2+BD2=PB2,
∴∠PDB=90°,
∴∠BDC=135°,
∴∠APC=∠CDB=135°,∵∠CPD=45°,
∴∠APC+∠CPD=180°,
∴A,P,D共线,
∴AD=AP+PD=5,
在RtADB中,AB=![]() .
.
(3)如图3中,作CD⊥CP,使得CD=![]() PC=
PC=![]() ,则PD=
,则PD=![]() ,
,
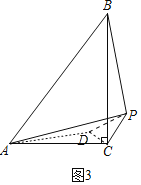
∵tan∠BAC=![]() ,
,
∴![]() ,
,
∵∠ACB=∠PCD=90°,
∴∠ACD=∠BCP,
∴△ACD∽△BCP,
∴![]() ,
,
∴![]() ,
,
∵![]() ,
,
∴![]() ,
,
∴PA的最大值为![]() .
.


科目:初中数学 来源: 题型:
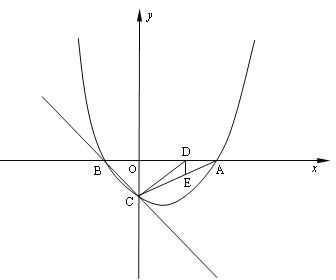
【题目】如图, 已知抛物线![]() 与y轴相交于C,与x轴相交于A、B,点A的坐标为(2,0),点C的坐标为(0,-1).
与y轴相交于C,与x轴相交于A、B,点A的坐标为(2,0),点C的坐标为(0,-1).
(1)求抛物线的解析式;
(2)点E是线段AC上一动点,过点E作DE⊥x轴于点D,连结DC,当△DCE的面积最大时,求点D的坐标;
(3)在直线BC上是否存在一点P,使△ACP为等腰三角形,若存在,求点P的坐标,若不存在,说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,无人机在空中C处测得地面A、B两点的俯角分别为60°、45°,如果无人机距地面高度CD为![]() 米,点A、D、E在同一水平直线上,则A、B两点间的距离是_____米.(结果保留根号)
米,点A、D、E在同一水平直线上,则A、B两点间的距离是_____米.(结果保留根号)

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某校为了了解学生“最喜爱的运动项目”的情况,随机抽取了部分学生进行问卷调查,规定每人从“篮球”、“羽毛球”、“自行车”、“游泳”和“其他”五个选项中必须选择且只能选择一个,并将调查结果绘制成如下两幅不完整的统计图表.
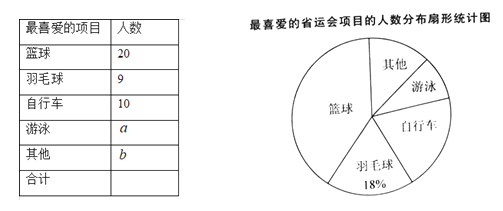
根据以上信息,请回答下列问题:
(1)这次调查的样本容量是 ,a+b= .
(2)扇形统计图中“自行车”对应的扇形的圆心角为 .
(3)若该校有1200名学生,估计该校最喜爱的省运会项目是篮球的学生人数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】将分别标有数字1,6,8的三张卡片(卡片除所标注数字外其他均相同)洗匀后,背面朝上放在桌面上.
(1)随机抽取一张卡片,抽到的卡片所标数字是偶数的概率为 ;
(2)随机抽取一张卡片,将卡片上标有的数字作为十位上的数字(不放回),再随机抽取一张卡片,将卡片上标有的数字作为个位上的数字,用列表或画树状图的方法求组成的两位数恰好是“68”的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某市水产养殖户进行小龙虾养殖.已知每千克小龙虾养殖成本为6元,在整个销售旺季的80天里,销售单价p(元/千克)与时间第t(天)之间的函数关系为: ,日销售量y(千克)与时间第t(天)之间的函数关系如图所示:
,日销售量y(千克)与时间第t(天)之间的函数关系如图所示:
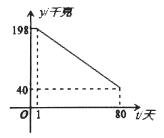
(1)求日销售量y与时间t的函数关系式?
(2)哪一天的日销售利润最大?最大利润是多少?
(3)该养殖户有多少天日销售利润不低于2400元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】程大位是我国明朝商人,珠算发明家.他60岁时完成的《直指算法统宗》是东方古代数学名著,详述了传统的珠算规则,确立了算盘用法.书中有如下问题:
一百馒头一百僧,大僧三个更无争,
小僧三人分一个,大小和尚得几丁.
意思是:有100个和尚分100个馒头,如果大和尚1人分3个,小和尚3人分1个,正好分完,大、小和尚各有多少人,下列求解结果正确的是( )

A. 大和尚25人,小和尚75人 B. 大和尚75人,小和尚25人
C. 大和尚50人,小和尚50人 D. 大、小和尚各100人
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,抛物线y=ax2+bx﹣2交x轴负半轴于点A(﹣1,0),与y轴交于B点.过B点的直线l交抛物线于点C(3,﹣1).过点C作CD⊥x轴,垂足为D.点P为x轴正半轴上的动点,过P点作x轴的垂线,交直线l于点E,交抛物线于点F.设P点的横坐标为t.
(1)求抛物线的解析式;
(2)连接OE,求△POE面积的最大值;
(3)连接DE,CF,是否存在这样的t值:以点C,D,E,F为顶点的四边形是平行四边形?请说明理由.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com