
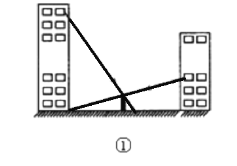
【题目】如图,某中学两座教学楼中间有个路灯,甲、乙两个人分别在楼上观察路灯顶端,视线所及如图①所示.根据实际情况画出平面图形如图②,CD⊥DF,AB⊥DF,EF⊥DF,甲从点C可以看到点G处,乙从点E恰巧可以看到点D处,点B是DF的中点,路灯AB高5.5米,DF=120米,BG=10.5米,求甲、乙两人的观测点到地面的距离的差.
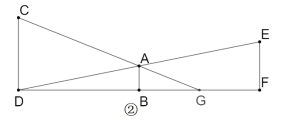
【答案】25.9(米)
【解析】
利用垂直的定义可证∠ABD=∠F,再利用有两组对应角相等的两三角形相似,可证得△DAB~△DEF,同理得△GAB~△GCD,再利用相似三角形的对应边成比例,就可求出EF,DG的长,然后求出CD的长即甲、乙两人的观测点到地面的距离的差.
∵AB⊥DF,EF⊥DF,
∴∠ABD=∠F=90°,
又∵∠EDF=∠ADB,
∴△DAB~△DEF,
同理得△GAB~△GCD,
∵点B是DF的中点,
∴DB=BF=![]() DF=
DF=![]() ×120=60,
×120=60,
∵![]()
∴EF=2AB=2x5.5=11,
∵BG=10.5,
∴DG=10.5+60=70.5
∴![]()
∴CD=![]() AB=
AB=![]() ×55≈36.9
×55≈36.9
∴甲、乙两人的观察点到地面的距离的差为:36.9-11=25.9(米).


 名校课堂系列答案
名校课堂系列答案科目:初中数学 来源: 题型:
【题目】如图,矩形![]() 中,
中,![]() ,
,![]() ,动点
,动点![]() 从
从![]() 点出发以
点出发以![]() /秒向终点
/秒向终点![]() 运动,动点
运动,动点![]() 同时从
同时从![]() 点出发以
点出发以![]() /秒按
/秒按![]()
![]() 的方向在边
的方向在边![]() ,
,![]() ,
,![]() 上运动,设运动时间为
上运动,设运动时间为![]() (秒),那么
(秒),那么![]() 的面积
的面积![]() 随着时间
随着时间![]() (秒)变化的函数图象大致为( )
(秒)变化的函数图象大致为( )
A. B.
B.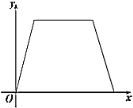 C.
C. D.
D.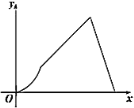
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,是根据九年级某班50名同学一周的锻炼情况绘制的条形统计图,下面关于该班50名同学一周锻炼时间的说法错误的是( )

A.平均数是6
B.中位数是6.5
C.众数是7
D.平均每周锻炼超过6小时的人数占该班人数的一半
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】春节前夕,某批发部从厂家购进A、B两种礼盒,已知购进2个A礼盒和3个B礼盒共花520元;购进3个A礼盒和2个B礼盒共花费480元.
(1)求A、B两种礼盒的单价分别是多少元?
(2)该批发部经理购进这两种礼盒恰好用去4800元购进A种礼盒最多18个,B种礼盒的数量不超过A种礼盒数量的2倍,共有几种进货方案?
(3)已知销售一个A种礼盒可获利10元,销售一个B种礼盒可获利18元,该店主决定每售出一个B种礼盒,为爱心公益基金捐款m元,每个A种礼盒的利润不变,在(2)的条件下,要使A、B两种礼盒全部售出后所有方案获利均相同,m的值应是多少?此时这个批发部获利多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】阅读理解:如图1,在△ABC中,当DE∥BC时可以得到三组成比例线段:① ![]() ;②
;② ![]() ;③
;③ ![]() .反之,当对应线段程比例时也可以推出DE∥BC.
.反之,当对应线段程比例时也可以推出DE∥BC.
理解运用:三角形的内接四边形是指顶点在三角形各边上的四边形.
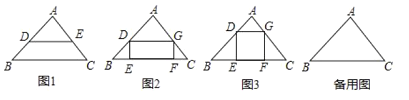
(1)如图2,已知矩形DEFG是△ABC的一个内接矩形,将矩形DEFG沿CB方向向左平移得矩形PBQH,其中顶点D、E、F、G的对应点分别为P、B、Q、H,在图2中画出平移后的图形;
(2)在(1)所得的图形中,连接CH并延长交BP的延长线于点R,连接AR.求证:AR∥BC;
(3)如图3,某小区有一块三角形空地,已知△ABC空地的边AB=400米,BC=600米,∠ABC=45°;准备在△ABC内建一个内接矩形广场DEFG(点E、F在边BC上,点D、G分别在边AB和AC上),三角形其余部分进行植被绿化,按要求欲使矩形DEFG的对角线EG最短,请在备用图中画出使对角线EG最短的矩形.并求出对角线EG的最短距离(不要求证明).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】我市某童装专卖店在销售中发现,一款童装每件进价为40元,若销售价为60元,每天可售出20件,为迎接“双十一”,专卖店决定采取适当的降价措施,以扩大销售量,经市场调查发现,如果每件童装降价1元,那么平均可多售出2件![]() 设每件童装降价x元
设每件童装降价x元![]() 时,平均每天可盈利y元.
时,平均每天可盈利y元.
![]() 写出y与x的函数关系式;
写出y与x的函数关系式;
![]() 当该专卖店每件童装降价多少元时,平均每天盈利400元?
当该专卖店每件童装降价多少元时,平均每天盈利400元?
![]() 该专卖店要想平均每天盈利600元,可能吗?请说明理由.
该专卖店要想平均每天盈利600元,可能吗?请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,正方形ABCD的边长为2,P为CD的中点,连结AP,过点B作BE⊥AP于点E,延长CE交AD于点F,过点C作CH⊥BE于点G,交AB于点H,连接HF.下列结论正确的是( )

A. CE=![]() B. EF=
B. EF=![]() C. cos∠CEP=
C. cos∠CEP=![]() D. HF2=EFCF
D. HF2=EFCF
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在△ABC中,若O为BC边的中点,则必有:AB2+AC2=2AO2+2BO2成立.依据以上结论,解决如下问题:如图,在矩形DEFG中,已知DE=4,EF=3,点P在以DE为直径的半圆上运动,则PF2+PG2的最小值为( )

A. ![]() B.
B. ![]() C. 34 D. 10
C. 34 D. 10
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com