
科目:初中数学 来源: 题型:解答题
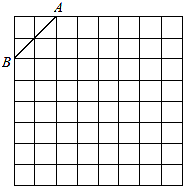 如图是规格为8×8的正方形网格,请在所给网格中按下列要求操作:
如图是规格为8×8的正方形网格,请在所给网格中按下列要求操作:查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,已知AB是⊙O的弦,∠B=30°,C是弦AB上的任意一点(不与点A、B重合),连接CO并延长交⊙O于点D,连接AD.
如图,已知AB是⊙O的弦,∠B=30°,C是弦AB上的任意一点(不与点A、B重合),连接CO并延长交⊙O于点D,连接AD.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
| x | … | 0 | 1 | 2 | 3 | 4 | … |
| y | … | 3 | 0 | -1 | 0 | 3 | … |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
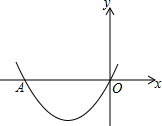 如图,在直角坐标系xOy中,若抛物线y=$\frac{1}{2}{x^2}$+2x交x轴的负半轴于A,以O为旋转中心,将线段OA按逆时针方向旋转α(0°<α≤360°),再沿水平方向向右或向左平移若干个单位长度,对应线段的一个端点正好落在抛物线的顶点处,请直接写出所有符合题意的α的值是30°或150°.
如图,在直角坐标系xOy中,若抛物线y=$\frac{1}{2}{x^2}$+2x交x轴的负半轴于A,以O为旋转中心,将线段OA按逆时针方向旋转α(0°<α≤360°),再沿水平方向向右或向左平移若干个单位长度,对应线段的一个端点正好落在抛物线的顶点处,请直接写出所有符合题意的α的值是30°或150°.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com