
| A. | 60° | B. | 95° | C. | 80° | D. | 75° |
分析 根据菱形的对角相等可得∠B=∠D,再根据等角三角形两底角相等,利用三角形的内角和等于180°表示出∠BAE和∠DAF,然后根据菱形的两邻角互补列式求解即可.
解答 解:如图所示: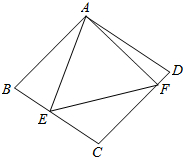 ∵四边形ABCD是菱形,△AEF为等边三角形,
∵四边形ABCD是菱形,△AEF为等边三角形,
∴∠B=∠D,AB=AD,AE=AF,∠EAF=60°,
∵正△AEF的边长与菱形ABCD的边长相等,
∴AB=AE,
∴AB=AE=AD=AF,
∴∠B=∠AEB,∠D=∠AFD,
∴∠BAE=180°-2∠AEB,∠DAF=180°-2∠AFD,
又∵∠EAF=60°,
∴180°-2∠AEB+60°+180°-2∠D+∠D=180°,
整理得,3∠AEB=240°,
解得∠AEB=80°.
故答案为:80°.
点评 本题考查了菱形的性质、等腰三角形两底角相等的性质、等边三角形的性质;根据菱形的邻角互补列出方程是解题的关键.


 点睛新教材全能解读系列答案
点睛新教材全能解读系列答案 小学教材完全解读系列答案
小学教材完全解读系列答案科目:初中数学 来源: 题型:解答题
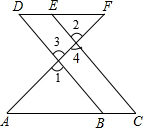 如图,点E在DF上,点B在AC上,∠1=∠2,∠C=∠D.
如图,点E在DF上,点B在AC上,∠1=∠2,∠C=∠D.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,∠1的同位角是∠EFG,∠1的内错角是∠BCD;
如图,∠1的同位角是∠EFG,∠1的内错角是∠BCD;查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com