
分析 (1)先根据题意画出图形,由AM+MB=AB得到2AB=20,从而可求得AB的长;
(2)分为点C在AB上和点C在AB的延长线上两种情况计算即可.
解答 解:(1)如图1所示:
根据题意可知:AM+MB+AB=20.
∵AM+MB=AB,
∴2AB=20.
∴AB=10.
(2)如图2所示:点C在AB的延长线上.
∵AB=10,BC=4,
∴AC=AB+BC=10+4=14.
∵N是AC的中点,
∴AN=$\frac{1}{2}AC$=$\frac{1}{2}×14$=7.
如图3所示;点C在AB上.
∵AB=10,BC=4,
∴AC=10-4=6.
∵N是AC的中点,
∴AN=$\frac{1}{2}AC$=$\frac{1}{2}×6$=3.
∴AN的长为3或7.
点评 本题主要考查的是两点间的距离,分类讨论是解题的关键.


科目:初中数学 来源: 题型:解答题
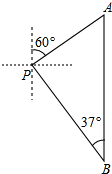 如图,小明从P处出发,沿北偏东60°方向行驶200米到达A处,接着向正南方向行驶一段时间到达B处.在B处观测到出发时所在的P处在北偏西37°方向上,这时P、B两点相距多少米?(精确到1米,参考数据:sin37°≈0.60,cos37°≈0.80,tan37°≈0.75,
如图,小明从P处出发,沿北偏东60°方向行驶200米到达A处,接着向正南方向行驶一段时间到达B处.在B处观测到出发时所在的P处在北偏西37°方向上,这时P、B两点相距多少米?(精确到1米,参考数据:sin37°≈0.60,cos37°≈0.80,tan37°≈0.75,查看答案和解析>>
科目:初中数学 来源: 题型:填空题
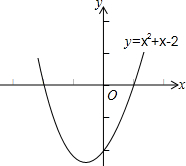 观察函数的图象.完成填空;
观察函数的图象.完成填空;查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | y=$\frac{1}{2}$(x-2)2+1 | B. | y=$\frac{1}{2}$(x-2)2-1 | C. | y=$\frac{1}{2}$(x+2)2+1 | D. | y=$\frac{1}{2}$(x+2)2-1 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com