
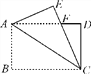
【题目】如图,矩形纸片ABCD中,AB=4,BC=6,将△ABC沿AC折叠,使点B落在点E处,CE交AD于点F,则DF的长等于_________.
【答案】![]()
【解析】分析:根据折叠的性质得到AE=AB,∠E=∠B=90°,易证Rt△AEF≌Rt△CDF,即可得到结论EF=DF;易得FC=FA,设FA=x,则FC=x,FD=6﹣x.在Rt△CDF中利用勾股定理得到关于x的方程x2=42+(6﹣x)2,解方程求出x,即可得到结论.
详解:∵矩形ABCD沿对角线AC对折,使△ABC落在△ACE的位置,∴AE=AB,∠E=∠B=90°.
又∵四边形ABCD为矩形,∴AB=CD,∴AE=DC,而∠AFE=∠DFC.
在△AEF与△CDF中,∵ ,∴△AEF≌△CDF(AAS),∴EF=DF;
,∴△AEF≌△CDF(AAS),∴EF=DF;
∵四边形ABCD为矩形,∴AD=BC=6,CD=AB=4.
∵Rt△AEF≌Rt△CDF,∴FC=FA,设FA=x,则FC=x,FD=6﹣x.在Rt△CDF中,CF2=CD2+DF2,即x2=42+(6﹣x)2,解得:x=![]() ,则FD=6﹣x=
,则FD=6﹣x=![]() .
.
故答案为:![]() .
.


科目:初中数学 来源: 题型:
【题目】学校艺术节要印制节目单,有两个印刷厂前来联系业务,他们的报价相同,甲厂的优惠条件是:按每份定价1.5元的八折收费,另收900元制版费;乙厂的优惠条件是:每份定价1.5元的价格不变,而900元的制版费则六折优惠.问:
(1)学校印制多少份节目单时两个印刷厂费用是相同的?
(2)学校要印制1500份节目单,选哪个印刷厂所付费用少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,分别以Rt△ABC的直角边AC及斜边AB向外作等边△ACD及等边△ABE.已知∠BAC=30°,EF⊥AB,垂足为F,连接DF.
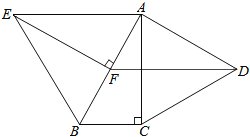
(1)试说明AC=EF;
(2)求证:四边形ADFE是平行四边形.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,数轴上A点表示数a,它与原点的距离是2个单位长度,B点表示数b,它与原点的距离是4个单位长度.
(1)![]() ;
;![]() ;
;
(2)已知甲从A处出发,同时乙从B处出发,设运动的时间为![]() (秒),
(秒),
①若甲向右,乙向左运动,速度均为2个单位/秒,当![]() 时,甲与原点的距离是 ;乙与原点的距离是 ;
时,甲与原点的距离是 ;乙与原点的距离是 ;
②若甲、乙均向左运动,甲的速度为m个单位/秒,乙的速度为n个单位/ 秒,当![]() 时,用代数式表示甲、乙所表示的数.
时,用代数式表示甲、乙所表示的数.
![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
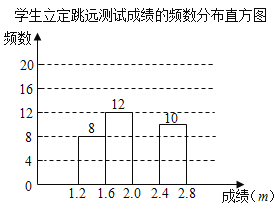
【题目】为了解某校八年级学生立定跳远水平,随机抽取该年级50名学生进行测试,并把测试成绩(单位:![]() )绘制成不完整的频数分布表和频数分布直方图.
)绘制成不完整的频数分布表和频数分布直方图.
学生立定路远测试成绩的频数分布表
分组 | 频数 |
|
|
| 12 |
|
|
| 10 |
请根据图表中所提供的信息,完成下列问题:
(1)求表中![]() ,
,![]() 的值;
的值;
(2)请把频数分布直方图补充完整;
(3)该校八年级共有800名学生,估计该年级学生立定跳远成绩在![]() 范围内的学生有多少人?
范围内的学生有多少人?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】我们知道,有理数包括整数、有限小数和无限循环小数,事实上,所有的有理数都可以化为分数形式(整数可看作分母为 ![]() 的分数),那么无限循环小数如何表示为分数形式呢?请看以下示例:
的分数),那么无限循环小数如何表示为分数形式呢?请看以下示例:
例:将 ![]() 化为分数形式.
化为分数形式.
由于 ![]() ,
,
设 ![]()
则 ![]()
![]() 得
得 ![]() ,
,
解得 ![]() ,于是得
,于是得 ![]() .
.
同理可得 ![]() ,
,![]() .
.
根据以上阅读,回答下列问题:(以下计算结果均用最简分数表示)
(![]() )
)![]() ,
,![]() ;
;
(![]() )将
)将 ![]() 化为分数形式,写出推导过程;
化为分数形式,写出推导过程;
(3)试比较 ![]() 与
与 ![]() 的大小:
的大小:![]()
![]() (填“
(填“![]() ”,“
”,“![]() ”或“
”或“![]() ”);
”);
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com