
【题目】已知一次函数y1=kx-2(k为常数,k≠0)和y2=x+1.
(1)当k=3时,若y1>y2,求x的取值范围.
(2)在同一平面直角坐标系中,若两函数的图像相交所形成的锐角小于15°,请直接写出k的取值范围.
【答案】(1)x>![]() ;(2)
;(2)![]() <k<
<k<![]() ,且k≠1
,且k≠1
【解析】
(1)解不等式3x-2>x+1即可;
(2)y2斜率为1,图象与x轴形成的角度为45°,若两函数的图像相交所形成的锐角小于15°,画出大致图象可判断出y1与x轴所形成的角度范围是30°到60°之间,根据特殊角的正弦值可得出k的取值范围.
解:(1)当k=3时,y1=3x-2.
根据题意,得3x-2>x+1,解得x>![]() .
.
(2)如图,
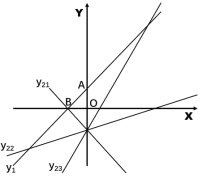
∵y2=x+1,
∴∠ABO=∠OBA=45°,
①若k<0,假设图象为y21,此时,两直线夹角一直大于45°,不符合题意,舍去;
②若k>0,假设图象为y22,此时,存在两直线夹角小于15°,由图象可得,当夹角达到最大15°时,y22与x轴夹角达到最小为30°,∴k>![]() ,当两直线平行时,无交点,此时k=1,不符合题意,舍去;当k>1时,当夹角达到最大15°时,y23与x轴夹角达到最大为60°,∴k<
,当两直线平行时,无交点,此时k=1,不符合题意,舍去;当k>1时,当夹角达到最大15°时,y23与x轴夹角达到最大为60°,∴k<![]() ,
,
综上所述,![]() <k<
<k<![]() ,且k≠1.
,且k≠1.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
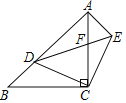
【题目】如图,在Rt△ACB中,∠ACB=90°,AC=BC,D是AB上的一个动点(不与点A,B重合),连接CD,将CD绕点C顺时针旋转90°得到CE,连接DE,DE与AC相交于点F,连接AE.下列结论:①△ACE≌△BCD;②若∠BCD=25°,则∠AED=65°;③DE2=2CFCA;④若AB=3![]() ,AD=2BD,则AF=
,AD=2BD,则AF=![]() .其中正确的结论是______.(填写所有正确结论的序号)
.其中正确的结论是______.(填写所有正确结论的序号)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,抛物线y=ax2+bx﹣5与坐标轴交于A(﹣1,0),B(5,0),C(0,﹣5)三点,顶点为D.
(1)请直接写出抛物线的解析式及顶点D的坐标;
(2)连接BC与抛物线的对称轴交于点E,点P为线段BC上的一个动点(点P不与B、C两点重合),过点P作PF∥DE交抛物线于点F,设点P的横坐标为m.
①是否存在点P,使四边形PEDF为平行四边形?若存在,求出点P的坐标;若不存在,说明理由.
②过点F作FH⊥BC于点H,求△PFH周长的最大值.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知A1,A2,A3,…An是x轴上的点,且OA1=A1A2=A2A3=…=An-1An=1,分别过点A1,A2,A3,…An作x轴的垂线交反比例函数y=![]() (x>0)的图象于点B1,B2,B3,…Bn,过点B2作B2P1⊥A1B1于点P1,过点B3作B3P2⊥A2B2于点P2……,记△B1P1B2的面积为S1,△B2P2B3的面积为S2……,△B6P6B7的面积为S6,则S1+S2+S3+…+S6=______________.
(x>0)的图象于点B1,B2,B3,…Bn,过点B2作B2P1⊥A1B1于点P1,过点B3作B3P2⊥A2B2于点P2……,记△B1P1B2的面积为S1,△B2P2B3的面积为S2……,△B6P6B7的面积为S6,则S1+S2+S3+…+S6=______________.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】2020年是脱贫攻坚、全面建设小康社会关键年.为响应党的号召,蓬溪县中职校向一所希望小学赠送文具1080件,现用A、B两种不同的包装箱进行包装,已知每个B型包装箱比A型包装箱多装15件文具,单独使用B型包装箱比单独使用A型包装箱可少用12个.问B型包装箱每个可以装多少件文具?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】甲、乙两车分别从![]() 两地同时出发,甲车匀速前往
两地同时出发,甲车匀速前往![]() 地,到达
地,到达![]() 地立即以另一速度按原路匀速返回到
地立即以另一速度按原路匀速返回到![]() 地,乙车匀速前往
地,乙车匀速前往![]() 地.设甲、乙两车距
地.设甲、乙两车距![]() 地的路程为
地的路程为![]() (千米),甲车行驶的时间为
(千米),甲车行驶的时间为![]() (小时),
(小时),![]() 与
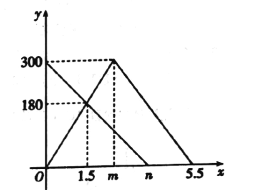
与![]() 之间的函数图像如图所示.
之间的函数图像如图所示.
(1)图中,![]() ,
,![]() ;
;
(2)求甲车返回时![]() 与
与![]() 之间的函数关系式,并写出自变量
之间的函数关系式,并写出自变量![]() 的取值范围;
的取值范围;
(3)在甲车返回到![]() 地的过程中,当
地的过程中,当![]() 为何值时,甲、乙两车相距190千米?
为何值时,甲、乙两车相距190千米?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com