Question

【题目】如图，二次函数y=x2+px+q（p<0）的图象与x轴交于A、B两点，与y轴交于点C（0，-1），△ABC的面积为。

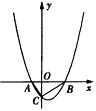
（1）求该二次函数的关系式；
（2）过y轴上的一点M（0，m）作y轴的垂线，若该垂线与△ABC的外接圆有公共点，求m的取值范围；
（3）在该二次函数的图象上是否存在点D，使四边形ACBD为直角梯形？若存在，求出点D的坐标；若不存在，请说明理由。

Answer 1

【答案】（1）y=;(2)- ≤m≤;(3) (， 或（-，9）

【解析】试题分析：（1）由△ABC的面积为，可得AB×OC=，又二次函数y=x2+px+q（p＜0）的图象与x轴交于A、B两点，与y轴交于点C（0，-1）可求得该二次函数的关系式；
（2）根据直线与圆的位置的位置关系确定m的取值范围．
（3）四边形ABCD为直角梯形，要分类讨论，即究竟那条边为底．可以分别以AC、BC为底进行讨论．

试题解析：

（1）由点C的坐标为（0，-1），得OC=1，
又∵△ABC的面积为，
∴，即，
由抛物线与y轴交于（0，-1），
得y=x2+px+g（p<0）中的q=-1，
则当y=0时，0=x2+px-1，设它的两个根为x1、x2，
则x1+x2=-p，x1x2=-1，且A、B两点的坐标为（x1，0）、（x2，0），
由直角坐标系上两点间的距离公式可得x2-x1=AB=，
∴，
∴x12+x22-2x1x2=，
∴x12+x22+2x1x2-4x1x2=，
∴（x1+x2）2-4x1x2=，即p2+4=，解得，
∵p<0，∴p=，
∴该抛物线的关系式为；

（2）设△ABC的外接圆交y轴于另一点D，如图
由得x1=2，，
∴，
连接AD，

在△ABC的外接圆中，
∵，
∴∠ADC=∠ABC，∠DAB=∠DCB，
∴△AOD∽△COB，
∴，
∴，
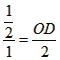∴DO=1，
∴CO=DO=1，
又∵AB⊥CD，
∴AB过△ABC外接圆的圆心，即AB为△ABC外接圆的直径，
∴△ABC外接圆的直径为，
∴直线与△ABC的外接圆相切，
∴；

（3）存在
∵AB是△ABC外接圆的直径，
∴∠ACB=90°，这时抛物线上必有点D，且当AD∥BC或BD∥AC时使四边形ACBD为直角梯形，
当AD∥BC时，可求得直线BC的关系式为，
∴直线AD的关系式为，
则它与抛物线的交点坐标为，
此时点D的坐标为，
当BD∥AC时，可求直线AC的关系式为y=-2x-1，
∴直线BD的关系式为y=-2x+4，
则它与抛物线的交点坐标为，
此时点D的坐标为，
∴当点D在或的位置时，四边形ACBD为直角梯形。