
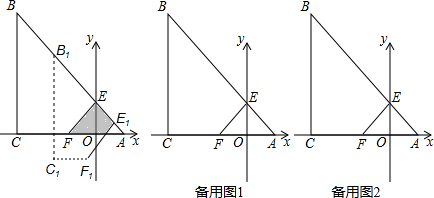
分析 (1)根据折叠后BE与EA所在直线重合推出EF=EA,OA=OE=2,可求出AE,EF的值.
(2)根据四边形BCFE与△AEF重叠的面积为直角梯形EFQE 1,由梯形的面积公式求出S与t的函数关系式,同理可证出其它三种情况;
(3)根据已知条件和勾股定理求出E1H的值,从而得出EH和EE1的值,再分三种情况讨论,当E1H=EE1时,当E1E=EH时,当E1H=EH时,求出x的值即可.
解答 解:(1)∵折叠后BE与EA所在直线重合,
∴EF⊥EA,
∵Rt△ABC中,AC=BC,
∴∠CAB=45°,
∴EF=EA,
∵A(2,0),
∴OA=OE=2,AE=2$\sqrt{2}$,
∴EF=2$\sqrt{2}$;
(2)如图1,当0≤t≤2$\sqrt{2}$时,
设F1E1与x轴交与点M,
∵平移时间为t(s),移动速度为每秒1个单位长度,
∴EE1=t,AE1=2$\sqrt{2}$-t,
∴ME1=2$\sqrt{2}$-t,
∴S=$\frac{1}{2}$(ME1+EF)EE1=$\frac{1}{2}$(2$\sqrt{2}$-t+2$\sqrt{2}$)t=-$\frac{1}{2}$t2+2$\sqrt{2}$t(0≤t≤2$\sqrt{2}$),
同理可得出其它函数解析式:
S=4(2$\sqrt{2}$≤t≤4$\sqrt{2}$)
S=-$\frac{1}{4}$t2+2$\sqrt{2}$t-4(4$\sqrt{2}$≤t≤6$\sqrt{2}$)
S=$\frac{1}{4}$t2-4$\sqrt{2}$t+32(6$\sqrt{2}$≤t≤8$\sqrt{2}$);
(3)根据题意得:
E1H=$\sqrt{(\frac{3\sqrt{2}}{2}t-2)^{2}+(2-\frac{\sqrt{2}}{2}t)^{2}}$=$\sqrt{5{t}^{2}-8\sqrt{2}t+8}$,EH=$\sqrt{2{t}^{2}-4\sqrt{2}t+8}$,EE1=$\sqrt{\frac{1}{2}{t}^{2}+\frac{1}{2}{t}^{2}}$=$\sqrt{{t}^{2}}$,
分三种情况:
当E1H=EE1时,4t2-8$\sqrt{2}$t+8=0,即t2-2$\sqrt{2}$t+2=0,
解得:t=$\sqrt{2}$;
当E1E=EH时,2t2-4$\sqrt{2}$t+8=t2,即t2-4$\sqrt{2}$t+8=0,
解得:t=2$\sqrt{2}$;
当E1H=EH时,5t2-8$\sqrt{2}$t+8=2t2-4$\sqrt{2}$t+8,即3t2-4$\sqrt{2}$t=0,
解得:t=$\frac{4\sqrt{2}}{3}$或0(不合题意,舍去),
综上:t=$\sqrt{2}$或2$\sqrt{2}$或$\frac{4\sqrt{2}}{3}$.
点评 本题综合考查的是分段函数的知识,二次函数的综合运用以及三角函数的应用,关键是根据题意画出相应的辅助线,注意分类讨论,不要漏解.


 阳光课堂课时优化作业系列答案
阳光课堂课时优化作业系列答案科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
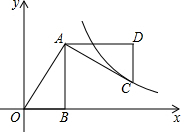 如图,平面直角坐标中,OB在x轴上,∠ABO=90°,点A的坐标为(2,4),将△AOB绕点A逆时针旋转90°,点O的对应点C恰好落在双曲线y=$\frac{k}{x}$(x>0)上,则k的值为( )
如图,平面直角坐标中,OB在x轴上,∠ABO=90°,点A的坐标为(2,4),将△AOB绕点A逆时针旋转90°,点O的对应点C恰好落在双曲线y=$\frac{k}{x}$(x>0)上,则k的值为( )| A. | 12 | B. | 10 | C. | 8 | D. | 6 |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
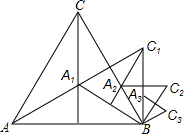 如图,点A1是面积为3的等边△ABC的两条中线的交点,以BA1为一边,构造等边△BA1C1,称为第一次构造;点A2是△BA1C1的两条中线的交点,再以BA2为一边,构造等边△BA2C2,称为第二次构造;以此类推,当第n次构造出的等边△BnAnCn的顶点Cn第一次落在线段AB上时,构造停止.则构造出的最后一个三角形的面积是$\frac{1}{27}$.
如图,点A1是面积为3的等边△ABC的两条中线的交点,以BA1为一边,构造等边△BA1C1,称为第一次构造;点A2是△BA1C1的两条中线的交点,再以BA2为一边,构造等边△BA2C2,称为第二次构造;以此类推,当第n次构造出的等边△BnAnCn的顶点Cn第一次落在线段AB上时,构造停止.则构造出的最后一个三角形的面积是$\frac{1}{27}$.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
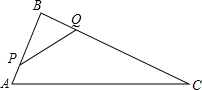 如图,在△ABC中,AB=8cm,BC=16cm,点P从点A开始沿AB向点B以2m/s的速度运动,点Q从点B开始沿BC边向点C以4cm/s的速度运动,如果P、Q分别从A、B同时出发,4秒后停止运动.则在开始运动后第几秒,△BPQ与△BAC相似?
如图,在△ABC中,AB=8cm,BC=16cm,点P从点A开始沿AB向点B以2m/s的速度运动,点Q从点B开始沿BC边向点C以4cm/s的速度运动,如果P、Q分别从A、B同时出发,4秒后停止运动.则在开始运动后第几秒,△BPQ与△BAC相似?查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com