
【题目】为了庆祝中华人民共和国成立70周年,某市决定开展“我和祖国共成长”主题演讲比赛,某中学将参加本校选拔赛的40名选手的成绩(满分为100分,得分为正整数且无满分,最低为75分)分成五组,并绘制了下列不完整的统计图表.
分数段 | 频数 | 频率 |
74.5~79.5 | 2 | 0.05 |
79.5~84.5 | m | 0.2 |
84.5~89.5 | 12 | 0.3 |
89.5~94.5 | 14 | n |
94.5~99.5 | 4 | 0.1 |
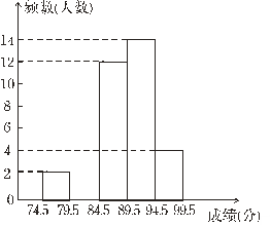
(1)表中m= ,n= ;
(2)请在图中补全频数直方图;
(3)甲同学的比赛成绩是40位参赛选手成绩的中位数,据此推测他的成绩落在 分数段内;
(4)选拔赛中,成绩在94.5分以上的选手,男生和女生各2人,学校从中随机确定2名选手参加全市决赛,恰好是一名男生和一名女生的概率是 .
【答案】(1)m=8, n=0.35;(2)详见解析;(3)84.5~89.5;(4)![]()
【解析】
(1)根据频率=频数÷总数求解可得;
(2)根据所求结果即可补全图形;
(3)根据中位数的概念求解可得;
(4)首先根据题意画出树状图,然后由表格即可求得所有等可能的结果与挑选的两位学生恰好是一男一女的情况,再利用概率公式求解即可求得答案.
解:(1)m=40×0.2=8,n=14÷40=0.35,
故答案为:8,0.35;
(2)补全图形如下: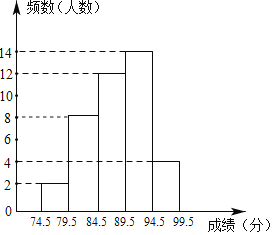
(3)由于40个数据的中位数是第20、21个数据的平均数,而第20、21个数据均落在84.5~89.5,
∴测他的成绩落在分数段84.5~89.5内,
故答案为:84.5~89.5.
(4)选手有4人,2名是男生,2名是女生. ,
,
恰好是一名男生和一名女生的概率为:![]() .
.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
【题目】中国古代有着辉煌的数学成就,《周髀算经》,《九章算术》,《海岛算经》,《孙子算经》等是我国古代数学的重要文献.
(1)小聪想从这4部数学名著中随机选择1部阅读,则他选中《九章算术》的概率为 ;
(2)某中学拟从这4部数学名著中选择2部作为“数学文化”校本课程学习内容,求恰好选中《九章算术》和《孙子算经》的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某城市绿化工程进行招标,现有甲、乙两个工程队投标,已知甲队单独完成这项工程需要60天.经测算:如果甲队先做20天,再由甲队、乙队合作12天,那么此时共完成总工作量的![]() .
.
(1)乙队单独完成这项工程需要多少天?
(2)甲队施工一天需付工程款4.5万元,乙队施工一天需付工程款2万元,该工程由甲乙两队合作若干天后,再由乙队完成剩余的工作,若要求完成此项工程的工程款不超过186万元,求甲、乙两队最多合作多少天?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】一次函数y=-x+1的图象与反比例函数![]() 的图象有一个交点是A(-1,n).
的图象有一个交点是A(-1,n).
(1)求反比例函数的解析式;
(2)M(d,![]() ),N(d,
),N(d,![]() )分别是一次函数和反比例函数图象上的两点,若
)分别是一次函数和反比例函数图象上的两点,若![]() ,求d的值.
,求d的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,平行四边形ABCD,AE⊥BC交点E,连接DE,F为DE上一点,且∠AFE=∠B=60°.
(1)求证:△ADF∽△DEC;
(2)若AE=3,AD=4,求EF的长.
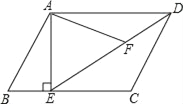
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,AB是半圆O的直径,D,E是半圆上任意两点,连结AD,DE,AE与BD相交于点C,要使△ADC与△ABD相似,可以添加一个条件.下列添加的条件其中错误的是( )
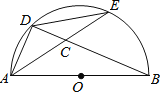
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】有一段6000米的道路由甲乙两个工程队负责完成.已知甲工程队每天完成的工作量是乙工程队每天完成工作量的2倍,且甲工程队单独完成此项工程比乙工程队单独完成此项工程少用10天.
(1)求甲、乙两工程队每天各完成多少米?
(2)如果甲工程队每天需工程费7000元,乙工程队每天需工程费5000元,若甲队先单独工作若干天,再由甲乙两工程队合作完成剩余的任务,支付工程队总费用不超过79000元,则两工程队最多可以合作施工多少天?
查看答案和解析>>
科目:初中数学 来源: 题型:
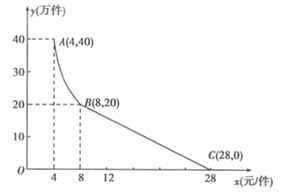
【题目】“净扬”水净化有限公司用160万元,作为新产品的研发费用,成功研制出了一种市场急需的小型水净化产品,已于当年投入生产并进行销售.已知生产这种小型水净化产品的成本为4元/件,在销售过程中发现:每年的年销售量![]() (万件)与销售价格x(元/件)的关系如图所示,其中AB为反比例函数图象的一部分,BC为一次函数图象的一部分.设公司销售这种水净化产品的年利润为z(万元).(注:若上一年盈利,则盈利不计入下一年的年利润;若上一年亏损,则亏损计作下一年的成本.)
(万件)与销售价格x(元/件)的关系如图所示,其中AB为反比例函数图象的一部分,BC为一次函数图象的一部分.设公司销售这种水净化产品的年利润为z(万元).(注:若上一年盈利,则盈利不计入下一年的年利润;若上一年亏损,则亏损计作下一年的成本.)
(1)请求出y(万件)与x(元/件)之间的函数关系式;
(2)求出第一年这种水净化产品的年利润z(万元)与x(元/件)之间的函数关系式,并求出第一年年利润的最大值;
(3)假设公司的这种水净化产品第一年恰好按年利润z(万元)取得最大值时进行销售,现根据第一年的盈亏情况,决定第二年将这种水净化产品每件的销售价格x(元)定在8元以上(![]() ),当第二年的年利润不低于103万元时,请结合年利润z(万元)与销售价格x(元/件)的函数示意图,求销售价格x(元/件)的取值范围.
),当第二年的年利润不低于103万元时,请结合年利润z(万元)与销售价格x(元/件)的函数示意图,求销售价格x(元/件)的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
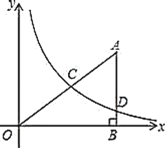
【题目】如图,在平面直角坐标系中,![]() 为坐标原点,
为坐标原点,![]() 的边
的边![]() 垂直
垂直![]() 轴于点
轴于点![]() ,反比例函数
,反比例函数![]()
![]() 的图象经过
的图象经过![]() 的中点
的中点![]() ,与边
,与边![]() 相交于点
相交于点![]() ,
,![]() .
.
(1)求反比例函数![]() 的解析式;
的解析式;
(2)求![]() 的值;
的值;
(3)经过![]() 、
、![]() 两点的直线的解析式是__________.
两点的直线的解析式是__________.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com