
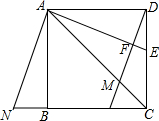
 已知正方形ABCD如图所示,连接其对角线AC,∠DAC的平分线AE交CD于点E,过点D作DM⊥AE于F,交AC于点M,共过点A作AN⊥AE交CB延长线于点N.
已知正方形ABCD如图所示,连接其对角线AC,∠DAC的平分线AE交CD于点E,过点D作DM⊥AE于F,交AC于点M,共过点A作AN⊥AE交CB延长线于点N.分析 (1)通过计算得到∠N=∠NAC=67.5°,所以AC=CN=3$\sqrt{2}$,根据三角形面积公式即可解决问题.
(2)在FA上截取FH=FE,连接DH,先证明△ADH≌△DCM,得AH=DM,再证明△ABN≌△ADE,得AN=AE,由此即可解决问题.
解答 (1)解:∵四边形ABCD是正方形,
∴AD=AB=BC=CD=3,∠DAB=∠ABC=∠BCD=∠DC=90°,∠CAB=∠CAD=∠ACB=45°,
∵AE平分∠DAC,
∴∠DAE=∠EAC=22.5°,
∵AE⊥AN,
∴∠NAE=90°,∠NAC=90°-∠CAE=67.5°,∠N=180°-∠NAC-∠CN=67.5°,
∴∠N=∠NAC
∴CA=CN=$\sqrt{A{B}^{2}+B{C}^{2}}$=$\sqrt{{3}^{2}+{3}^{2}}$=3$\sqrt{2}$,
∴S△ACN=$\frac{1}{2}$×CN×AB=$\frac{1}{2}$×$3\sqrt{2}$×3=$\frac{9\sqrt{2}}{2}$.
(2)在FA上截取FH=FE,连接DH.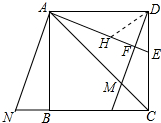
∵AE⊥DM,
∴DH=DE,
∴∠DHE=∠DEH=90°-∠DAE=67.5°,
∴∠MDC=∠HDF=90°-∠DEA=22.5°,
∴∠ADH=90°-∠HDE=45°,
∴∠ADH=∠MCD,∠DAH=∠MDC,
在△ADH和△DCM中,
$\left\{\begin{array}{l}{∠DAH=∠CDM}\\{∠ADH=∠DCM}\\{AD=DC}\end{array}\right.$,
∴△ADH≌△DCM,
∴AH=DM,
在△ABN和△ADE中,
$\left\{\begin{array}{l}{∠NAB=∠DAE}\\{AB=AD}\\{∠ABN=∠ADE}\end{array}\right.$,
∴△ABN≌△ADE,
∴AN=AE,
∴AN=AH+HE=DM+2EF.
点评 本题考查正方形的性质、全等三角形的判定和性质、解题的关键是通过计算求出角的度数,发现相等的角,学会添加辅助线构造全等三角形,属于中考常考题型.


 七星图书口算速算天天练系列答案
七星图书口算速算天天练系列答案科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
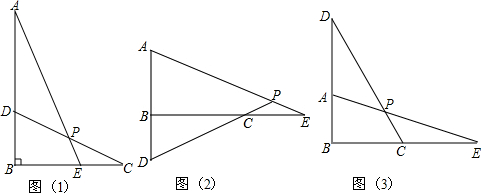
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 65° | B. | 60° | C. | 45° | D. | 70° |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
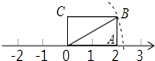 如图,矩形OABC的边OA长为2,边AB长为1,OA在数轴上,以原点O为圆心,对角线OB的长为半径画弧,交数轴于一点,则这个点表示的实数是$±\sqrt{5}$.
如图,矩形OABC的边OA长为2,边AB长为1,OA在数轴上,以原点O为圆心,对角线OB的长为半径画弧,交数轴于一点,则这个点表示的实数是$±\sqrt{5}$.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com