
李明准备进行如下操作实验,把一根长40cm的铁丝剪成两段,并把每段首尾相连各围成一个正方形.
(1)要使这两个正方形的面积之和等于58cm2,李明应该怎么剪这根铁丝?
(2)李明认为这两个正方形的面积之和不可能等于48cm2,你认为他的说法正确吗?请说明理由.
【考点】一元二次方程的应用.
【专题】几何图形问题.
【分析】(1)设剪成的较短的这段为xcm,较长的这段就为(40﹣x)cm.就可以表示出这两个正方形的面积,根据两个正方形的面积之和等于58cm2建立方程求出其解即可;
(2)设剪成的较短的这段为mcm,较长的这段就为(40﹣m)cm.就可以表示出这两个正方形的面积,根据两个正方形的面积之和等于48cm2建立方程,如果方程有解就说明李明的说法错误,否则正确.
【解答】解:(1)设剪成的较短的这段为xcm,较长的这段就为(40﹣x)cm,由题意,得
(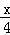 )2+(
)2+(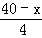 )2=58,
)2=58,
解得:x1=12,x2=28,
当x=12时,较长的为40﹣12=28cm,
当x=28时,较长的为40﹣28=12<28(舍去).
答:李明应该把铁丝剪成12cm和28cm的两段;
(2)李明的说法正确.理由如下:
设剪成的较短的这段为mcm,较长的这段就为(40﹣m)cm,由题意,得
(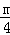 )2+(
)2+(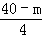 )2=48,
)2=48,
变形为:m2﹣40m+416=0,
∵△=(﹣40)2﹣4×416=﹣64<0,
∴原方程无实数根,
∴李明的说法正确,这两个正方形的面积之和不可能等于48cm2.
【点评】本题考查了列一元二次方程解实际问题的运用,一元二次方程的解法的运用,根的判别式的运用,解答本题时找到等量关系建立方程和运用根的判别式是关键.


 名校课堂系列答案
名校课堂系列答案科目:初中数学 来源: 题型:
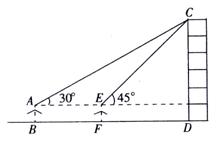
小敏同学测量一建筑物CD的高度,她站在B处仰望楼顶C,测得仰角为30°,再往建筑物方向走30m,到达点 F处测得楼顶C的仰角为45°(B,F,D在同一条直线上)。一直小敏的眼睛与地面距离为1.5m,求这栋建筑物CD的高度(参考数据:
F处测得楼顶C的仰角为45°(B,F,D在同一条直线上)。一直小敏的眼睛与地面距离为1.5m,求这栋建筑物CD的高度(参考数据: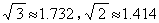 ,结果保留整数)
,结果保留整数)
 |
查看答案和解析>>
科目:初中数学 来源: 题型:
如图为二次函数y=ax2+bx+c(a≠0)的图象,对称轴是x=1,则下列说法:①b>0;②2a+b=0;③4a﹣2b+c>0;④3a+c>0;⑤m(ma+b)<a+b(常数m≠1).其中正确的个数为( )
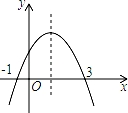
A.2 B.3 C.4 D.5
查看答案和解析>>
科目:初中数学 来源: 题型:
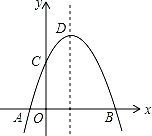
如图,抛物线y=﹣x2+2x+m+1交x轴于点A(a,0)和B(b,0),交y轴于点C,抛物线的顶点为D,下列四个命题:
①当x>0时,y>0;
②若a=﹣1,则b=3;
③抛物线上有两点P(x1,y1)和Q(x2,y2),若x1<1<x2,且x1+x2>2,则y1>y2;
④点C关于抛物线对称轴的对称点为E,点G,F分别在x轴和y轴上,当m=2时,四边形EDFG周长的最小值为6 .
.
其中真命题的序号是 .
查看答案和解析>>
科目:初中数学 来源: 题型:
甲同学的身高为1.5m,某一时刻他的影长为1m,此时一塔影长为20 m,则该塔高为___m.
超速行驶是引发交通事故的主要原因之一,上周末,小明和三位同学尝试用自己所学的知识检测车速,如图8,观测点设在A处,离娄新高速的距离(AC)为30 m,这时,一辆小轿车由西向东匀速行驶,测得此车从B处行驶到C处所用的时间为4s,∠BAC=75°.
(1)求B、C两点的距离;
(2)请判断此车是否超过了娄新高速100km/h的限制速度?(计算时距离精确到
1 m,参考数据:sin 75°≈0.965 9,cos 75°≈0.258 8,tan 75°≈3.732,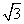 ≈1.732,100 km/h≈27.8m/s)
≈1.732,100 km/h≈27.8m/s)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com