练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情
    5．已知正比例函数y=（2-k）x的图象经过第二、四象限，求函数y=-kx的图象经过哪些象限？

    分析 根据正比例函数的性质：当k＞0时，图象经过一、三象限，y随x的增大而增大；当k＜0时，图象经过二、四象限，y随x的增大而减小，可得答案．

    解答 解：由正比例函数y=（2-k）x的图象经过第二、四象限，得
    2-k＜0．
    解得k＞2．
    两边都乘以-1，得
    -k＜-2．
    由-k＜-2，得
    函数y=-kx的图象经过二四象限．

    点评 本题考查了正比例函数的性质，它是经过原点的一条直线．当k＞0时，图象经过一、三象限，y随x的增大而增大；当k＜0时，图象经过二、四象限，y随x的增大而减小．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：解答题

    15．先阅读下面的例题，再完成作业．
    例题．解不等式（3x-2）（2x+1）＞0．
    解：由有理数的乘法法则可知“两数相乘，同号得正”．因此可得①$\left\{\begin{array}{l}{3x-2＞0}\\{2x+1＞0}\end{array}\right.$ 或②$\left\{\begin{array}{l}{3x-2＜0}\\{2x+1＜0}\end{array}\right.$，解不等式组①得x＞$\frac{2}{3}$，解不等式组②得x＜-$\frac{1}{2}$，所以不等式（3x-2）（2x+1）＞0的解集是x＜-$\frac{1}{2}$或x＞$\frac{2}{3}$．
    （1）求不等式$\frac{x+2}{3x+5}$＜0的解集；
    （2）例题和（1）的解法过程体现了数学中的什么思想？

    查看答案和解析>>

    科目：初中数学 来源： 题型：选择题

    16．△ABC中，∠A：∠B：∠C=2：3：4，则∠A的度数为（　　）
    A．35°B．40°C．70°D．110°

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

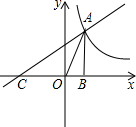    13．如图，在平面直角坐标系中，直线$y=x+\frac{k}{2}$与双曲线$y=\frac{k}{x}$在第一象限交于点A，与x轴交于点C，AB⊥x轴，垂足为B，此时点B（1，0）．求：
    （1）求两个函数解析式；
    （2）求△AOC的周长．

    查看答案和解析>>

    科目：初中数学 来源： 题型：填空题

    20．计算：3$\sqrt{5}$-（$\sqrt{5}$-$\sqrt{6}$）-$\sqrt{6}$=2$\sqrt{5}$．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    3．如图1，已知△ABC为等边三角形，D、E、F分别在边BC、CA、AB上，且△DEF也是等边三角形．
    （1）求证：AF=BD；
    （2）若△ABC的边长为2，求△DEF面积的最小值；
    （3）如图2，若△ABC和△FDE都改成等腰三角形，且顶角∠BAC=∠DFE，D是BC的中点，求证：DF∥AC．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    10．如图，已知△ABC中，∠C=90°，将△ACB绕点A顺时针旋转一个角度得△ADE，连接BE、CD，延长CD交BE于点F，求证：BF=EF．

    查看答案和解析>>

    科目：初中数学 来源： 题型：填空题

    7．已知二次函数y=ax2+bx+c（a≠0）的图象如图所示，下列由5个结论：①abc＜0；②b＜a+c；③4a+2b+c＞0；④2c＜3b；⑤a+b＞m（am+b）（m≠1）．其中正确的结论有①③④⑤．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    8．有一条公路连接A、B两地，一个骑行俱乐部上午9点从A地出发到达B地后返回，图中折线表示骑车人离A地的距离与时间的函数关系．有一辆客车9时从B地出发，以60千米/小时的速度为匀速行驶，图中的粗线表示客车离A地的距离与时间的函数关系．
    （1）A、B两地相距60千米，骑车人最快速度是45千米/小时；
    （2）设骑车人离A地的距离为y1，客车离A地的距离为y2，时间为x，分别求出9点到10点之间二者的函数关系式；
    （3）若客车到达A地后立即返回B地（乘客上下车停留时间忽略不计），在原图上画出客车返程中离A地的距离与时间的函数图象，求出函数关系式，并求出客车与骑车人第二次相遇的时间．
    （4）若客车以原速度往返于两地（乘客上下车停留时间忽略不计），客车和骑车人还会相遇几次？直接写出相遇的时间．

    查看答案和解析>>

    同步练习册答案