练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情
    6．2-1+$\frac{\sqrt{27}}{\sqrt{3}}$=3$\frac{1}{2}$．

    分析 原式利用负整数指数幂法则，以及二次根式除法法则计算即可得到结果．

    解答 解：原式=$\frac{1}{2}$+3=3$\frac{1}{2}$，
    故答案为：3$\frac{1}{2}$

    点评 此题考查了二次根式的除法，以及负整数指数幂，熟练掌握运算法则是解本题的关键．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：解答题

    14．阅读以下材料，解答问题：
    例：设y=x2-4x+2，求y的最值．
    解：y=x2-4x+2=x2-2•2•x+22-2=（x-2）2-2
    ∵（x-2）2≥0
    ∴（x-2）2-2≥-2，即y有最小值是-2，
    问题：（1）设y=x2-6x-1，求y的最值．
    （2）设y=-x2+8x+1，求y的最值．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    15．已知x3+x2+x+1=0，求x2012的值．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

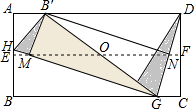    12．数学活动课上，老师组织各学习小组同学动手操作，大胆猜想并加以验证．
    动手操作：
    如图，将长与宽的比是2：1的矩形纸片ABCD对折，使得点B与点A重合，点C与点D重合，然后展开，得到折痕EFBC边上存在一点G，将角B沿GH折叠，点B落到AD边上的点B′处，点B在AD上边上的点B′处，点H在AB边上；将角C沿GD折叠，点C恰好落到B′G上的点C′处．HG和DG分别交于EF于点M和点N，B′G交EF于点O，连接B′M，B′N．
    提出猜想：
    ①“希望”小组猜想：HG⊥DG；
    ②“奋斗”小组猜想：B′N⊥DG；
    ③“创新”小组猜想：四边形B′MGN是矩形．
    独立思考：
    （1）请你验证上述学习小组猜想的三个结论；（写出解答过程）
    （2）假如你是该课堂的一名成员，请你在现有图形中，找出一个和四边形B′MGN面积相等的四边形．（直接写出其名称，不必证明）

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

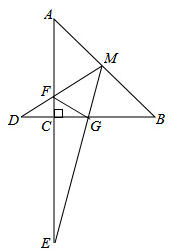    1．如图，M为等腰直角三角形ABC斜边AB的中点，AC=4，MD交AC于F，交BC延长线于D，ME交BC于G，交AC延长线于E，且AF=3，∠DMG=45°．
    （1）写出图中的三对相似三角形．
    （2）连接FG，求FG的长．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

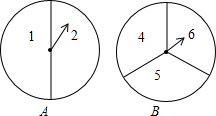    11．如图，有两个可以自由转动的均匀转盘A、B，分别被分成2等份和3等份，每份内均都有数字．小明和小亮用这两个转盘做游戏，游戏规则如下：分别转动转盘A和B，两个转盘停止后，将两个指针所指份内的数字相加（如果指针恰好停在等分线上，那么重转一次，直到指针指向某一份为止），若和为偶数，则小明获胜；如果和为奇数，那么小亮获胜．
    （1）求小明获胜的概率；
    （2）这个游戏对双方公平吗？请说明理由．

    查看答案和解析>>

    科目：初中数学 来源： 题型：选择题

    18．若a＜b，则下列不等式的变形中不正确的是（　　）
    A．a+5＜b+5B．$\frac{a}{5}$$＜\frac{b}{5}$C．5a-1＜5b-1D．5-a＜5-b

    查看答案和解析>>

    科目：初中数学 来源： 题型：选择题

    15．下列命题是真命题的是（　　）
    A．两条不相交的直线就是平行线
    B．过任意一点可以作已知直线的一条平行线
    C．过直线外任意一点作已知直线的垂线，可以作无数条
    D．直线外一点与直线上各点所连接的所有线段中，垂线段最短

    查看答案和解析>>

    科目：初中数学 来源： 题型：选择题

    16．小于5的正整数有（　　）个．
    A．1B．2C．3D．4

    查看答案和解析>>

    同步练习册答案