
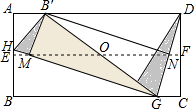
 ��ѧ����ϣ���ʦ��֯��ѧϰС��ͬѧ���ֲ��������벢������֤��
��ѧ����ϣ���ʦ��֯��ѧϰС��ͬѧ���ֲ��������벢������֤������ ��1�����ɡ�BGH=��B��GH����DGC=��DGB�伴��֤������ֻҪ֤����B��DG�ǵ��������μ��ɣ���ֻҪ֤��OM=OB��=OG���ɣ�
��2�����ݵ��������ε����ʡ����ε����ʼ��ɽ�����⣮
��� ��1���⣺�ߡ�BGH=��B��GH����DGC=��DGB�䣬
��2��B��GH+2��DGB��=180�㣬
���B��GH+��DGB��=90�㣬
���DGH=90�㼴HG��DG�ʢ���ȷ��
��AD��BC��
���B��DG=��DGC=��DGB�䣬
��B��D=B��G
��AD��EF��BC��
AE=EB��DF=FC��
��DN=NG��B��O=OG��
��B��N��DG�ʢ���ȷ��
��OM��BG��
���OMG=��MGB=��MGO��
��MO=OG=OB�䣬
���B��MG��ֱ�������Σ�
���B��MG=90�㣬
�ߡ�B��MG=��B��NG=��NGM=90�㣬
���ı���B��MGN�Ǿ��Σ��ʢ���ȷ��
��2�����ۣ��ı���B��MND���ı���B��MGN�������ȣ�
���ɣ��ߡ�B��DG�ǵ��������Σ�DN=NG��
��S��B��ND=S��B��NG��
��S��B��MG=S��B��MN��
��S�ı���B��MGN=S�ı���B��MND��
���� ���⿼�鷭�۱任�����������ε��ж������ʡ�ֱ�������ε��ж�����������Ĺؼ������÷��۲����ԣ������п��������ͣ�


 ��У����ϵ�д�
��У����ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ������
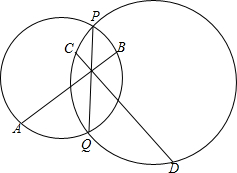 ��ͼ��PQΪ��Բ�Ĺ����ң�MΪPQ��һ�㣬AB��CD�ֱ�����Բ�����������ཻ��M����֤��A��C��B��D�ĵ㹲Բ��
��ͼ��PQΪ��Բ�Ĺ����ң�MΪPQ��һ�㣬AB��CD�ֱ�����Բ�����������ཻ��M����֤��A��C��B��D�ĵ㹲Բ���鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | a+1��a+2��a+3��a��0�� | B�� | �����߶εı���4��6��8 | ||
| C�� | 3cm��8cm��10cm | D�� | 3a��5a��2a+1��a��0�� |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
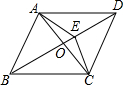 ��ͼ��������ABCD�У���ABC=70�㣬AC��BD�ཻ�ڵ�O��E��OD��һ�㣬����AE=DE��������˵������ȷ���ǣ�������
��ͼ��������ABCD�У���ABC=70�㣬AC��BD�ཻ�ڵ�O��E��OD��һ�㣬����AE=DE��������˵������ȷ���ǣ�������| A�� | ��E�ǡ�ACD������ | B�� | ��DBC=35�� | C�� | CE=DE | D�� | ��ABO�ա�CBO |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com