
����Ŀ����֪����x�ķ���kx2+��2k+1��x+2=0��
��1����֤������kȡ�κ�ʵ��ʱ����������ʵ������
��2����������y=kx2+��2k+1��x+2ͼ����x����������ĺ������Ϊ��������kΪ������ʱ����P��a��y1����Q��1��y2���Ǵ��������ϵ����㣬��y1��y2�����Ϻ���ͼ��ȷ��ʵ��a��ȡֵ��Χ��
��3����֪������y=kx2+��2k+1��x+2������㣬����������꣮
���𰸡���1��֤������������2��a��1��a����4����3�������ߺ�����㣨0��2��������2��0����
�������������������1���������ۣ��÷�����һԪһ�η��̺�һԪ���η���������������÷���ΪһԪ���η���ʱ�������б�ʽ����0����������ʵ������
��2��ͨ����kx2+��2k+1��x+2=0�õ�k=1���ɴ˵õ��������߽���ʽΪy=x2+3x+2�����ͼ��ش����⣮
��3����������õ�kx2+��2k+1��x+2-y=0��������ɴ��г�����x��y�ķ����飬ͨ���ⷽ������øö������꣮
�����������1��֤�����ٵ�k=0ʱ������Ϊx+2=0������x=��2��������ʵ������
�ڵ�k��0ʱ���ߡ�=��2k+1��2��4k��2=��2k��1��2��0��������0��
������kȡ�κ�ʵ��ʱ����������ʵ������
��2���⣺��y=0����kx2+��2k+1��x+2=0��
�����x��һԪ���η��̣���x1=��2��x2=��![]() ��
��
�߶��κ�����ͼ����x����������ĺ������Ϊ��������kΪ��������
��k=1��
��������߽���ʽΪy=x2+3x+2��
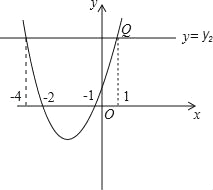
��ͼ��õ�����y1��y2ʱ��a��1��a����4��
��3���������kx2+��2k+1��x+2��y=0���������k��x2+2x��+x��y+2=0�������
��![]() ��
��
���![]() ��
��![]() ��
��
���Ը������ߺ�����㣨0��2��������2��0����


 ��������һ���þ�ϵ�д�
��������һ���þ�ϵ�д� Сѧ��10����Ӧ����ϵ�д�
Сѧ��10����Ӧ����ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ij�̵깺��45��A��Ʒ��20��B��Ʒ������800Ԫ������60��A��Ʒ��35��B��Ʒ������1100Ԫ��
��1��A��B������Ʒ�ĵ��۷ֱ��Ƕ���Ԫ��
��2����֪���̵깺��B��Ʒ�ļ����ȹ���A��Ʒ������2����4���������Ҫ����A��B������Ʒ���ܼ���������32�����Ҹ��̵깺��A��B������Ʒ���ܷ��ò�����296Ԫ����ô���̵��м��ֹ�����������д�����п��ܵĹ�������.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��Ϊ�˸��ø��ƺ�����ˮ�ʣ����۹�˾��������10̨��ˮ�����豸![]() ����A��B�����ͺŵ��豸������ÿ̨�ļ۸��´�����ˮ�����±��������飺����һ̨A���豸�ȹ���һ̨B���豸��2��Ԫ������2̨A���豸�ȹ���3̨B���豸��6��Ԫ��
����A��B�����ͺŵ��豸������ÿ̨�ļ۸��´�����ˮ�����±��������飺����һ̨A���豸�ȹ���һ̨B���豸��2��Ԫ������2̨A���豸�ȹ���3̨B���豸��6��Ԫ��
A�� | B�� | |
�۸� | a | b |
������ˮ�� | 240 | 200 |
![]() ��a��b��ֵ��
��a��b��ֵ��
![]() ���۹�˾��Ԥ�㹺����ˮ�����豸���ʽ���105��Ԫ������Ϊ�ù�˾���ļ��ֹ�����
���۹�˾��Ԥ�㹺����ˮ�����豸���ʽ���105��Ԫ������Ϊ�ù�˾���ļ��ֹ�����
![]() ��
��![]() �������£���ÿ��Ҫ������ˮ��������2040�֣�Ϊ�˽�Լ�ʽ�����Ϊ���۹�˾���һ����ʡǮ�Ĺ�����
�������£���ÿ��Ҫ������ˮ��������2040�֣�Ϊ�˽�Լ�ʽ�����Ϊ���۹�˾���һ����ʡǮ�Ĺ�����
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��ABΪ��O��ֱ������CΪ��O��һ�㣬����BAC=��CAM������C��ֱ��l��ֱ������AM������Ϊ��D��
��1�����ж�CD����O��λ�ù�ϵ����˵�����ɣ�
��2����ֱ��l��AB���ӳ����ཻ�ڵ�E����O�İ뾶Ϊ3��������CAB=30�㣬��CE�ij���

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��Ϊ�˽���������2018�������������ÿ���¾������������ز������������1000�˵������Ϣ������������ͼ��ʾ��Ƶ��ֱ��ͼ������ͼ���ṩ����Ϣ��������˵����ÿ��ֵ�������ֵ�����������ֵ�����ٳ������������¾�������60Ԫ��80Ԫ��������ࣻ���¾�������160Ԫ����160Ԫ�����ϵ�����ռ��������������10%�������������1000���У�������һ�����ϵ��˵��¾����ѳ���75Ԫ����Ϊ�����������ܸ�����Żݣ���ز�����ȷ��һ���ۿ۱����ƻ�ʹ30%���ҵ��˻���Żݣ���ô�����dz������������¾����Ѵﵽ100Ԫ����100Ԫ�����ϵ��������ۿۣ�

A.1��B.2��C.3��D.4��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
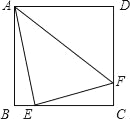
����Ŀ����ͼ����������ABCD�У���E��F�ֱ��ڱ�BC��CD�ϣ����AE=4��EF=3��AF=5����ô������ABCD���������_____��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����![]() �ǡ�
�ǡ�![]() �ڵ�һ�㣬����
�ڵ�һ�㣬����![]() ��
��![]() �ڵ�
�ڵ�![]() �ڵ�
�ڵ�![]() ����
����![]() .
.
![]() ��֤:
��֤: ![]() ;
;
![]() ��ͼ�ڣ���
��ͼ�ڣ���![]() ������
������![]() ��һ�㣬��
��һ�㣬��![]() ���߶�
���߶�![]() ��һ�㣬��
��һ�㣬��![]() ����
����![]() .���߶�
.���߶�![]() �ij�.
�ij�.
![]() ��ͼ�ۣ���
��ͼ�ۣ���![]() ����
����![]() �Ƶ�
�Ƶ�![]() ��ÿ��
��ÿ��![]() ���ٶ�˳ʱ����ת��
���ٶ�˳ʱ����ת��![]() ���
���![]() ��ʼ�Ƶ�
��ʼ�Ƶ�![]() ��ÿ��
��ÿ��![]() ���ٶ�˳ʱ����ת��
���ٶ�˳ʱ����ת��![]() ��ת
��ת![]() ��ֹͣ����ʱ
��ֹͣ����ʱ![]() Ҳ��ֹ֮ͣ��ת����ת�����У�
Ҳ��ֹ֮ͣ��ת����ת�����У�![]() ����ֱ����
����ֱ����![]() ����ֱ�ߵĽ����Ϊ
����ֱ�ߵĽ����Ϊ![]() ����ֱ����
����ֱ����![]() ����ֱ�ߵĽ����Ϊ
����ֱ�ߵĽ����Ϊ![]() .��
.��![]() ��ת����ʱ��
��ת����ʱ��![]() ��
��

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
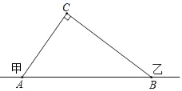
����Ŀ���ڼ״����Ҵ����һ����·����C����Ҫ���ƣ���֪��C�빫·�ϵ�ͣ��վA�ľ���Ϊ300�ף��빫·�ϵ���һͣ��վB�ľ���Ϊ400�ף���CA��CB����ͼ��ʾ��Ϊ�˰�ȫ��������Ƶ�C��Χ�뾶250��Χ�ڲ��ý��룬�ʣ��ڽ��б���ʱ����·AB���Ƿ���Σ�գ��Ƿ���Ҫ��ʱ������������ѧ����֪ʶ���Խ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
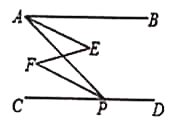
����Ŀ����������֤��.
��ͼ��![]() ��
��![]() ������
������![]() ����֤��
����֤��![]() .���ڱ���С��������֤���ģ����㽫����֤�����̲�������.
.���ڱ���С��������֤���ģ����㽫����֤�����̲�������.
֤����![]() ��
��![]() ������(��֪)
������(��֪)
![]() .(________________________________)
.(________________________________)
![]() .(________________________________)
.(________________________________)
![]() ��(��֪)
��(��֪)
![]() ��(��������)
��(��������)
��_______________=_______________.
![]() .(________________________________)
.(________________________________)
![]() .(________________________________)
.(________________________________)
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com