
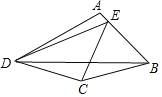
【题目】四边形ABCD中,AB=BC=CD,∠ABC=60°,点E在AB上,∠AED=∠CEB,AD=5,DE+CE=![]() ,则BD的长为_____.
,则BD的长为_____.
【答案】7
【解析】
连接AC,延长DE至F,使EF=CE,作正三角形ADG,使B、G分别在AD两侧,连接AF、BF、BG,证明△BEF≌△BEC(SAS),可证得△ABF是等边三角形,得出AF=AB,∠BAF=60°,证明△DAF≌△GAB(SAS),得出BG=DF=DE+EF=DE+CE=![]() ,证明△ABC是等边三角形,得出AC=BC=DC,∠ACB=60°,得出点C是△ABD的外心,由圆周角定理得出∠ADB=
,证明△ABC是等边三角形,得出AC=BC=DC,∠ACB=60°,得出点C是△ABD的外心,由圆周角定理得出∠ADB=![]() ∠ACB=30°,证出∠BDG=∠ADB+∠ADG=90°,由勾股定理即可得出答案.
∠ACB=30°,证出∠BDG=∠ADB+∠ADG=90°,由勾股定理即可得出答案.
连接AC,延长DE至F,使EF=CE,作正三角形ADG,使B、G分别在AD两侧,连接AF、BF、BG,如图所示:
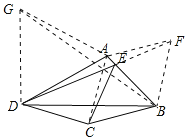
∵∠AED=∠CEB,∠BEF=∠AED,
∴∠BEF=∠AED=∠CEB,
在△BEF和△BEC中,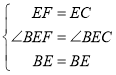 ,
,
∴△BEF≌△BEC(SAS),
∴∠ABF=∠ABC=60°,BF=BC=AB,
∴△ABF是等边三角形,
∴AF=AB,∠BAF=60°,
∵△ADG是等边三角形,
∴∠ADG=∠DAG=60°=∠BAF,AG=AD=5,
∴∠DAF=∠DAB+∠BAF=∠DAB+∠DAG=∠GAB,
在△DAF和△GAB中,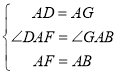 ,
,
∴△DAF≌△GAB(SAS),
∴BG=DF=DE+EF=DE+CE=![]() ,
,
∵AB=BC,∠ABC=60°,
∴△ABC是等边三角形,
∴AC=BC=DC,∠ACB=60°,
∴点C是△ABD的外心,
∴∠ADB=![]() ∠ACB=30°,
∠ACB=30°,
∴∠BDG=∠ADB+∠ADG=90°,
∴BD=![]() ;
;
故答案为:7.


 夺冠金卷全能练考系列答案
夺冠金卷全能练考系列答案科目:初中数学 来源: 题型:
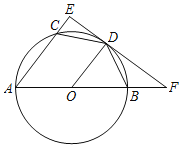
【题目】如图,已知AB为⊙O的直径,点C、D在⊙O上,CD=BD,E、F是线段AC、AB的延长线上的点,并且EF与⊙O相切于点D.
(1)求证:∠A=2∠BDF;
(2)若AC=3,AB=5,求CE的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】图1是一种折叠门,由上下轨道和两扇长宽相等的活页门组成,整个活页门的右轴固定在门框
上,通过推动左侧活页门开关;图2是其俯视图简化示意图,已知轨道![]() ,两扇活页门的宽
,两扇活页门的宽![]() ,点
,点![]() 固定,当点
固定,当点![]() 在
在![]() 上左右运动时,
上左右运动时,![]() 与
与![]() 的长度不变(所有结果保留小数点后一位).
的长度不变(所有结果保留小数点后一位).
(1)若![]() ,求
,求![]() 的长;
的长;
(2)当点![]() 从点
从点![]() 向右运动60
向右运动60![]() 时,求点
时,求点![]() 在此过程中运动的路径长.
在此过程中运动的路径长.
(参考数据:sin50°≈0.77, cos50°≈0.64, tan50°≈1.19, π取3.14)

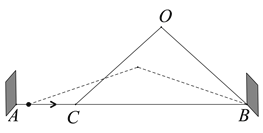
图1 图2
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,![]() 是☉
是☉![]() 的直径,
的直径,![]() 为☉
为☉![]() 上一点,
上一点,![]() 是半径
是半径![]() 上一动点(不与
上一动点(不与![]() 重合),过点
重合),过点![]() 作射线
作射线![]() ,分别交弦
,分别交弦![]() ,
,![]() 于
于![]() 两点,过点
两点,过点![]() 的切线交射线
的切线交射线![]() 于点
于点![]() .
.
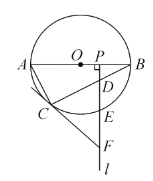
(1)求证:![]() .
.
(2)当![]() 是
是![]() 的中点时,
的中点时,
①若![]() ,判断以
,判断以![]() 为顶点的四边形是什么特殊四边形,并说明理由;
为顶点的四边形是什么特殊四边形,并说明理由;
②若![]() ,且
,且![]() ,则
,则![]() _________.
_________.
查看答案和解析>>
科目:初中数学 来源: 题型:
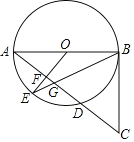
【题目】如图,在⊙O中,AB是⊙O的直径,F是弦AD的中点,连结OF并延长OF交⊙O于点E,连结BE交AD于点G,延长AD至点C,使得GC=BC,连结BC.
(1)求证:BC是⊙O的切线.
(2)⊙O的半径为10,sinA=![]() ,求EG的长.
,求EG的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
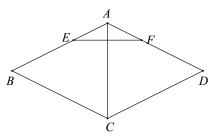
【题目】如图,在菱形ABCD中,AC为对角线,点E,F分别在AB,AD上,BE=DF,连接EF.
(1)求证:AC⊥EF;
(2)延长EF交CD的延长线于点G,连接BD交AC于点O,若BD=4,tanG=![]() ,求AO的长.
,求AO的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】小亮一家在一湖泊中游玩,湖泊中有一孤岛,妈妈在孤岛P处观看小亮与爸爸在湖中划船(如图所示).小船从P处出发,沿北偏东60°方向划行200米到A处,接着向正南方向划行一段时间到B处.在B处小亮观测到妈妈所在的P处在北偏西37°的方向上,这时小亮与妈妈相距多少米(精确到1米)?
(参考数据:sin37°≈0.60,cos37°≈0.80,tan37°≈0.75,![]() ≈1.41,
≈1.41,![]() ≈1.73)
≈1.73)

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,在矩形ABCD中,AB<BC,点E为对角线AC上的一个动点,连接BE,DE,过E作EF⊥BC于F.设AE=x,图1中某条线段的长为y,若表示y与x的函数关系的图象大致如图2所示,则这条线段可能是图1中的( )
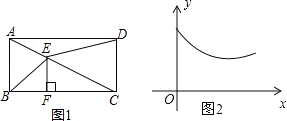
A.线段BEB.线段EFC.线段CED.线段DE
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com