
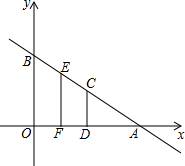
 如图,平面直角坐标系中,直线AB解析式为:y=-
如图,平面直角坐标系中,直线AB解析式为:y=-
| ||
| 3 |
| 3 |
| ||
| 3 |
| 3 |
| 3 |
| 3 |
| 3 |
| 1 |
| 2 |
| ||
| 2 |
| 1 |
| 2 |
| 3 |
| 2 |
| 1 |
| 2 |
| ||
| 2 |
| 3 |
3
| ||
| 4 |
| 1 |
| 2 |
| 3 |
| 4 |
| 3 |
| 4 |
3
| ||
| 4 |
| ||
| 3 |
| 3 |
| 3 |
| ||
| 3 |
| 3 |
| 3 |
| 3 |
| 3 |
| 3 |
|
|
| 3 |
| 4 |
3
| ||
| 4 |
| 3 |
| 3 |
| ||
| 3 |
|
|
| 3 |
| 4 |
| ||
| 4 |
| 3 |
| 3 |
| 3 |
| 4 |
3
| ||
| 4 |
| 3 |
| 4 |
| ||
| 4 |


 暑假接力赛新疆青少年出版社系列答案
暑假接力赛新疆青少年出版社系列答案科目:初中数学 来源: 题型:
查看答案和解析>>
科目:初中数学 来源: 题型:
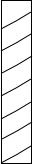 如图,有一根高为2m的圆柱形木材,它的底面周长为0.3m.为了营造喜庆的气氛,小颖想用一根彩带从圆木的底向顶均匀地缠绕7圈,一直缠到起点的正上方为止.小颖至少要准备多长的一根彩带?
如图,有一根高为2m的圆柱形木材,它的底面周长为0.3m.为了营造喜庆的气氛,小颖想用一根彩带从圆木的底向顶均匀地缠绕7圈,一直缠到起点的正上方为止.小颖至少要准备多长的一根彩带?查看答案和解析>>
科目:初中数学 来源: 题型:
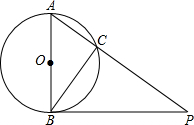 如图,已知AB是⊙O的直径,PB是⊙O的切线,PA交⊙O于C,AB=3cm,PB=4cm,则BC长为( )
如图,已知AB是⊙O的直径,PB是⊙O的切线,PA交⊙O于C,AB=3cm,PB=4cm,则BC长为( ) | A、5cm | B、2.4cm |
| C、3.6cm | D、1.8cm |
查看答案和解析>>
科目:初中数学 来源: 题型:
查看答案和解析>>
科目:初中数学 来源: 题型:
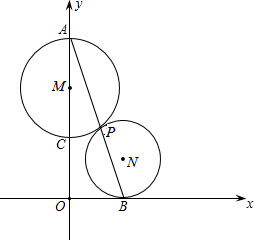 如图,⊙M与⊙N切于点P,经过点P的直线AB交⊙M于点A,交⊙N于点B,以经过⊙M直径AC所在直线为y轴,经过点B的直线为x轴建立平面直角坐标系,
如图,⊙M与⊙N切于点P,经过点P的直线AB交⊙M于点A,交⊙N于点B,以经过⊙M直径AC所在直线为y轴,经过点B的直线为x轴建立平面直角坐标系,查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com