
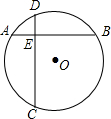
 如图,⊙O中弦AB⊥CD于E,AE=2,EB=6,ED=3,则⊙O的半径为$\frac{\sqrt{65}}{2}$.
如图,⊙O中弦AB⊥CD于E,AE=2,EB=6,ED=3,则⊙O的半径为$\frac{\sqrt{65}}{2}$. 分析 作OG⊥CD于G,OF⊥AB于F,由相交弦定理得出DE•CE=AE•BE,求出CE,得出CD,由垂径定理得出得EG,证出四边形OGEF为矩形,得出OF=EG=$\frac{1}{2}$,根据勾股定理计算即可,
解答 解:作OG⊥CD于G,OF⊥AB于F,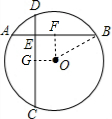 连接OB,
连接OB,
由相交弦定理得:DE•CE=AE•BE,即3×CE=2×6,
∴CE=4,
∴CD=CE+DE=7,
∵OF⊥AB,
∴DG=$\frac{1}{2}$DC=$\frac{7}{2}$,
∴EG=DG-DE=$\frac{1}{2}$,
∵OF⊥AB,AB=AE+BE=8,
∴BF=$\frac{1}{2}$AB=4,
∵OG⊥CD,OF⊥AB,CD⊥AB,
∴∠OGE=∠GEF=∠OFE=90°,
∴四边形OGEF为矩形,
∴OF=EG=$\frac{1}{2}$,
在Rt△OBF中,OF=$\frac{1}{2}$,BF=4,
根据勾股定理得:OB=$\sqrt{O{F}^{2}+B{F}^{2}}$=$\frac{\sqrt{65}}{2}$,
故答案为:$\frac{\sqrt{65}}{2}$.
点评 此题考查了相交弦定理、垂径定理、勾股定理、矩形的判定与性质,根据图形作出相应的辅助线是解本题的关键.


 一线名师权威作业本系列答案
一线名师权威作业本系列答案科目:初中数学 来源: 题型:解答题
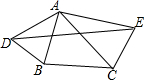 如图,△ABC中,AB=6,AC=8,分别以AB、AC为一边向外作等腰△ADB和等腰△ACE,AD=AB,AE=AC,且∠DAB=∠EAC=x,∠BAC=y(其中2x+y<180°).
如图,△ABC中,AB=6,AC=8,分别以AB、AC为一边向外作等腰△ADB和等腰△ACE,AD=AB,AE=AC,且∠DAB=∠EAC=x,∠BAC=y(其中2x+y<180°).查看答案和解析>>
科目:初中数学 来源: 题型:填空题
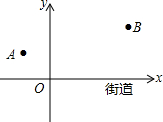 去年“双11”购物节的快递量暴增,某快递公司要在街道旁设立一个派送还点,向A、B两居民区投送快递,派送点应该设在什么地方,才能使它到A、B的距离之和最短?快递员根据实际情况,以街道为x轴,建立了如图所示的平面直角坐标系,测得坐标A(-2,2)、B(6,4),则派送点的坐标是($\frac{2}{3}$,0).
去年“双11”购物节的快递量暴增,某快递公司要在街道旁设立一个派送还点,向A、B两居民区投送快递,派送点应该设在什么地方,才能使它到A、B的距离之和最短?快递员根据实际情况,以街道为x轴,建立了如图所示的平面直角坐标系,测得坐标A(-2,2)、B(6,4),则派送点的坐标是($\frac{2}{3}$,0).查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | $\frac{1}{2}$ | B. | $\frac{3}{2}$ | C. | 1 | D. | $\frac{2}{3}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
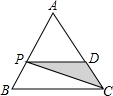 如图,P为等边三角形ABC中AB边上的动点,沿A→B的方向运动,到达点B时停止,过P作PD∥BC.设AP=x,△PDC的面积为y,则y关于x的函数图象大致为( )
如图,P为等边三角形ABC中AB边上的动点,沿A→B的方向运动,到达点B时停止,过P作PD∥BC.设AP=x,△PDC的面积为y,则y关于x的函数图象大致为( )| A. | 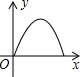 | B. | 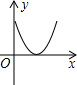 | C. | 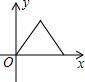 | D. | 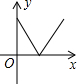 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com