
����Ŀ����֪���κ���y��ax��x��3��+c��a��0��0��x��3��������������y��![]() ��x��0��k��0��ͼ����ͼ1��ʾ����������y��
��x��0��k��0��ͼ����ͼ1��ʾ����������y��![]() ��x��0��k��0����ͼ����P��m��n����PM��x�ᣬ����ΪM��PN��y�ᣬ����ΪN����OM��ON��12����1����k��ֵ��
��x��0��k��0����ͼ����P��m��n����PM��x�ᣬ����ΪM��PN��y�ᣬ����ΪN����OM��ON��12����1����k��ֵ��
��2��ȷ�����κ���y��ax��x��3��+c��a��0��0��x��3���Գ��ᣬ�����㵱aȡ��1ʱ���κ��������ֵ�����ú�����ĸc��ʽ�ӱ�ʾ��
��3����c��0ʱ��������������x�����������֮��ľ��룮
��4����ͼ2����a��1ʱ��������y��ax��x��3��+c��a��0��0��x��3����һʱ��ǡ�þ���P�㣬�Ҵ�ʱ��������˫����y��![]() ��x��0��k��0������ֻ��һ��������P����ͼ2��ʾ�������Dz����Ѵ�ʱ�̵�c����c1����ֱ��д��������y��ax��x��3��+c��a��0��0��x��3����ͼ����˫����y��
��x��0��k��0������ֻ��һ��������P����ͼ2��ʾ�������Dz����Ѵ�ʱ�̵�c����c1����ֱ��д��������y��ax��x��3��+c��a��0��0��x��3����ͼ����˫����y��![]() ��x��0��k��0����ͼ����һ��������ʱc��ȡֵ��Χ��
��x��0��k��0����ͼ����һ��������ʱc��ȡֵ��Χ��

���𰸡�(1)k��12����2 x��![]() �����ֵΪ
�����ֵΪ![]() +c����3��3����4����������
+c����3��3����4����������
��������
��1����OM��ON=12����k=OM��ON��������⣻
��2��y=ax��x-3��+c�ĶԳ���Ϊx=![]() =
=![]() ����a=-1ʱ������y=ax��x-3��+c=-x��x-3��+c��������⣻
����a=-1ʱ������y=ax��x-3��+c=-x��x-3��+c��������⣻
��3����c=0ʱ����ʱ��y=0����ax��x-3��=0����a��0x��x-3��=0��������⣻
��4����c��c1��c=c1��c��c1��c��4����������ֱ���⼴�ɣ�
�⣺��1����OM��ON��12����k��OM��ON��12��
��2��y��ax��x��3��+c�ĶԳ���Ϊx����![]() ��
��![]() ��
��
��a����1ʱ������y��ax��x��3��+c����x��x��3��+c��
��y����x2��3x+c������x+![]() ��2+
��2+![]() +c��
+c��
���ʱ���κ���y����x��x��3��+c��a��0��0��x��3�������ֵΪ![]() +c��
+c��
��3����c��0ʱ�����κ���y��ax��x��3��+c��ax��x��3����a��0��0��x��3����
��ʱ��y��0����ax��x��3����0����a��0x��x��3����0��
��x��0��3��
����κ���y��ax��x��3����x�����������Ϊ��0��0���ͣ�3��0����
����������x�����������֮��ľ���Ϊ3��
��4���ٵ�c��c1ʱ��
������y����x��x��3��+c��ͼ����˫����y��![]() û�й����㣻
û�й����㣻
�ڵ�c��c1ʱ��
������y����x��x��3��+c��a��0��0��x��3����ͼ����˫����y��![]() ��Ψһ������P��
��Ψһ������P��
�۵�c��c1ʱ��
����������ƽ�ƣ����������Ҷ˵���������˫������ʱ���������ʱ��B������Ϊ��3��c1����c1��4��
�൱c1��c��4ʱ����������˫���������������㣻
�ܵ�c��4ʱ��������y����x��x��3��+c��a��0��0��x��3����ͼ���˫����ʼ����һ�������㣻
���Ե�c��c1ʱ��c��4ʱ��������y����x��x��3��+c��a��0��0��x��3����ͼ���˫����ʼ����һ�������㣮



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��Ϊ�˴���������У���ֹ2019��3����������17�Һ�����Է�鷿�������ѿ��ţ�ij�鷿Ϊ�˽�����Ķ����������������˲��ֶ�����һ���ڽ���ͼ��Ĵ��������Ƴ���ͼ��������ͳ��ͼ����
���߽���ͼ��Ĵ���ͳ�Ʊ�
����ͼ��Ĵ��� | 1�� | 2�� | 3�� | 4�� | 5�μ����� |
���� | 7 | 13 | a | 10 | 3 |
�������ͳ��ͼ���е���Ϣ������������⣺
��1��a���� ����b���� ����
��2���������ݵ�����Ϊ�� ������λ��Ϊ�� ����
��3�����������ͳ��ͼ�еġ�4�Ρ�����Ӧ��Բ�ĽǵĶ�����
��4����ͳ�Ƹ��鷿һ�ܹ���2000λ��ͬ�Ķ��ߣ��������ϵ���������������һ���ڽ���ͼ�顰4�μ����ϡ��Ķ���������

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��ABΪ��O��ֱ����CΪ��O��һ�㣬��ABC��ƽ���߽���O�ڵ�D��DE��BC�ڵ�E��
��1�����ж�DE���O��λ�ù�ϵ����˵�����ɣ�
��2������D��DF��AB�ڵ�F����BE=3![]() ��DF=3����ͼ����Ӱ���ֵ������
��DF=3����ͼ����Ӱ���ֵ������

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����ABC����ADE���ǵ���ֱ�������Σ���BAC����DAE��90�����ı���ACDE��ƽ���ı��Σ�CE��AD�ڵ�F����BD�ڵ�G���ף�����λͬѧ���������з��ۺõ����ۣ���CE��BD�����ҵõ����ۣ���CDAE��EFCG�����жϼף�����λͬѧ�Ľ����Ƿ���ȷ����˵�����ɣ�
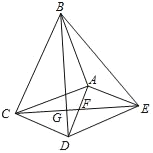
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ������ABC�У�BC��AC��5��AB��8��CDΪAB�ߵĸߣ���A��x���ϣ���B��y���ϣ���C�ڵ�һ���ޣ���A��ԭ���������x��������ÿ��1����λ�����ٶ��˶������B��֮��y���»�����������ABC��ƽ���ڻ��������˶�ʱ��Ϊt�룬��B����ԭ��ʱֹͣ�˶�
��1������OC���߶�OC�ij���t�ı仯���仯����OC���ʱ��t��____��
��2������ABC�ı���������ƽ��ʱ��t��____��
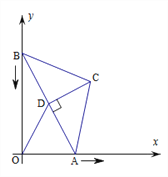
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ���к졢���������ӣ��������װ�б�ŷֱ�Ϊ1��2��3��5���ĸ����ƺ�����װ�б��Ϊ1��2��3���������ס���������������Ϸ����Ϸ����Ϊ���״Ӻ������ÿ������һ��С���Ҵӻƺ�����ÿ������һ��С����������֮��Ϊ���������ʤ��������ʤ��
��1�������б�����״ͼ�ķ��������ʤ�ĸ��ʣ�
��2�����������Ϸ����Լס���˫����ƽ������ƽ����˵�����ɣ�������ƽ���ԸĶ�������е�һ��С��ı�ţ�ʹ��Ϸ����ƽ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ƽ��ֱ������ϵ![]() �У�ֱ��
�У�ֱ��![]() ��
��![]() �ᡢ
�ᡢ![]() ��ֱ��ڵ�
��ֱ��ڵ�![]() ��
��![]() ��������
��������![]() ������
������![]() ������
������![]() ����ƽ��5����λ���ȣ��õ���
����ƽ��5����λ���ȣ��õ���![]() ��
��
��1�����![]() �����ꣻ
�����ꣻ
��2���������ߵĶԳ��
��3�������������߶�![]() ǡ��һ�������㣬��Ϻ���ͼ����
ǡ��һ�������㣬��Ϻ���ͼ����![]() ��ȡֵ��Χ��
��ȡֵ��Χ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ������������ӽ���������������ܵ����㷺��ע������Ҳ�ڸ���ѧУ��չ�˴��о�������������Ϸ����У����ijУ�Դ�����ϲ�����������������飬���ռ�����Ϣ����ͳ�ƣ����������������в�������ͳ��ͼ���������ͳ��ͼ���ṩ����Ϣ����������⣺
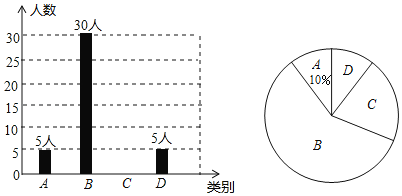
ͼ��A��ʾ����ϲ������B��ʾ��ϲ������C��ʾ��һ������D��ʾ����ϲ������
��1������������������� ���ˣ�����ͳ��ͼ��B��������Ӧ������Բ�ĽǵĶ���Ϊ�� ��������ȫ����ͳ��ͼ��
��2������У����ѧ��1800�ˣ�������������������Ƹ�Уѧ����A���ж����ˣ�
��3����A��5���У��պ���3��Ů��2�����������������ȡ����ͬѧ��������ɫ������״ͼ���б���������鵽������ѧ���Ա���ͬ�ĸ��ʣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��������ABCD�ı߳�Ϊ2����������ΪS1����CDΪб��������ֱ�������Σ��Ըõ���ֱ�������ε�һ��ֱ�DZ�Ϊ�������������Σ���������ΪS2���������մ˹��ɼ�����ȥ����S2018��ֵΪ��������
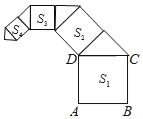
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com