
����Ŀ���Ķ����⣬���ش����⣺
��x1��x2�Ƿ���ax2+bx+c��0������ʵ����������ax2+bx+c��a��x��x1����x��x2������ax2+bx+c��ax2��a��x1+x2��x+ax1x2������b����a��x1+x2����c��ax1x2���ɴ˿ɵ�һԪ���η��̵ĸ���ϵ����ϵ��x1+x2����![]() ��x1x2��
��x1x2��![]() �����������������֪��Τ�ﶨ����
�����������������֪��Τ�ﶨ����
��1����֪m��n�Ƿ���x2��x��100��0������ʵ���������ⷽ����m2+n2��ֵ��
��2����x1��x2��x3���ǹ���x�ķ���x��x��2��2��t������ʵ��������x1��x2��x3��
��x1x2+x2x3+x3x1��ֵ������x3��x1�����ֵ��
���𰸡���1��201����2����4����![]()
��������
��1���ɸ���ϵ���Ĺ�ϵ�ȵó�m+n��1��mn����100����������ȫƽ����ʽ�ı��οɵô𰸣�
��2����������ã�x��x��2��2��t����x��x1����x��x2����x��x3��������ʽ���߷ֱ��������ٱȽ϶�Ӧ���ϵ���ɵô𰸣�
�����ɢٵó��Ľ������x1+x3��4��x2��x3x1��4����x1+x3��x2��Ȼ����![]() ��
��![]() ��4x3x1���䷽���ó�
��4x3x1���䷽���ó�![]() �����ֵ���ٿ�ƽ������������ƽ�������ɣ�
�����ֵ���ٿ�ƽ������������ƽ�������ɣ�
�⣺��1����m��n�Ƿ���x2��x��100��0������ʵ����
��m+n��1��mn����100
��m2+n2����m+n��2��2mn
��12��2������100��
��201��
��2����������ã�x��x��2��2��t����x��x1����x��x2����x��x3��
��x3��4x2+4x��t��x3����x1+x2+x3��x2+��x1x2+x2x3+x3x1��x��x1x2x3
��x1+x2+x3��4��x1x2+x2x3+x3x1��4��x1x2x3��t
��x1x2+x2x3+x3x1��ֵΪ4��
�ڡ�x1+x2+x3��4
��x1+x3��4��x2
��x1x2+x2x3+x3x1��4
��x3x1��4����x1+x3��x2
��![]() ��
��![]() ��4x3x1
��4x3x1
��![]() ��
��![]() ��4[4����x1+x3��x2]
��4[4����x1+x3��x2]
����3![]() +8x2
+8x2
����3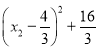 ��
��![]()
�൱x2��![]() ʱ��x3��x1�����ֵΪ��
ʱ��x3��x1�����ֵΪ��![]() ��
��![]() ��
��
��x3��x1�����ֵΪ![]() ��
��



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ������һ��92��94��96����������m��94��96�����ͨ����ؼ��㲢�Ƚϣ����֣���������ƽ�����ϴ����С����m��ֵ�����ǣ�������
A.91B.92C.95D.98
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��Ϊ����ʵ����������ƶ�����ߣ�A��B���Ǿ�����C��D�������ͷ�����֧��ũ����������֪A��B���ǹ��з���500�֣�����A�Ƿ��ϱ�B����100�֣���A����C��D�����˷��ϵķ��÷ֱ�Ϊ20Ԫ/�ֺ�25Ԫ/�֣���B����C��D�����˷��ϵķ��÷ֱ�Ϊ15Ԫ/�ֺ�24Ԫ/�֣���C����Ҫ����240�֣�D����Ҫ����260�֣�
��1��A�Ǻ�B�Ǹ��ж��ٶַ��ϣ�
��2�����A������C�����x�֣����˷�ΪyԪ������������˷ѣ�
��3�����ڸ������ͣ�ʹA������C����˷�ÿ�ּ���a��0��a��6��Ԫ����ʱ�������˲���ʹ���˷����٣�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��ƽ��ֱ������ϵ�У�����ABCD�ı�AB:BC��3:2����A��3��0����B��0��6���ֱ���x�ᣬy���ϣ�����������![]() (x��0)��ͼ����D����
(x��0)��ͼ����D����![]() ֵΪ�� ��
ֵΪ�� ��
A. ��14 B. 14 C. 7 D. ��7
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
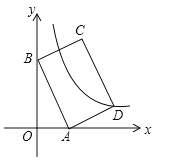
����Ŀ����ͼ1���ڡ�ABC�У�AB��AC����BAC��120������D��E�ֱ��ڱ�AB��AC�ϣ�AD��AE������DC����M��P��N�ֱ�ΪDE��DC��BC���е㣮
��1���۲����
ͼ1�У��߶�PM��PN��������ϵ���� ������MPN�Ķ������� ����
��2��̽��֤��
�ѡ�ADE�Ƶ�A��ʱ�뷽����ת��ͼ2��λ�ã�����MN��BD��CE���жϡ�PMN����״����˵�����ɣ�
��3����չ����
�ѡ�ADE�Ƶ�A��ƽ����������ת����AD��4��AB��8����ֱ��д����PMN�����ȡֵ��Χ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
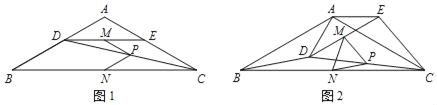
����Ŀ����ͼ��������ABCD�У���B��60����AB��2��MΪ��AB���е㣬NΪ��BC��һ���㣨�����B�غϣ�������BMN��ֱ��MN�۵���ʹ��B���ڵ�E��������DE��CE������CDEΪ����������ʱ��BN�ij�Ϊ_____��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����![]() �У�
��![]() ��
��![]() ��
��![]() ���ϵĶ���(�����
���ϵĶ���(�����![]() �غ�)����
�غ�)����![]() ��
��![]() ���ڵ�ֱ�߷��ۣ��õ�
���ڵ�ֱ�߷��ۣ��õ�![]() ������
������![]() ���������жϣ�
���������жϣ�

�ٵ�![]() ʱ��
ʱ��![]()
�ڵ�![]() ʱ��
ʱ��![]()
�۵�![]() ʱ��
ʱ��![]() ��
��
��![]() ���ȵ���Сֵ��1��
���ȵ���Сֵ��1��
������ȷ���ж���______(������ȷ���۵����)
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ�����ž��ÿ��ٷ�չ����������Խ��Խ�ܵ����ǵĹ�ע��ijУΪ���˽���ܼ��š����������֪ʶ���ռ��������������˲���ѧ������������Ϊ���dz��˽������˽������˽�����������˽������࣬����������Ƴ�����������������ͳ��ͼ�������ͳ��ͼ�ش��������⣺
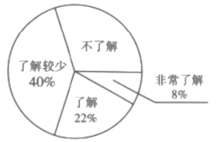
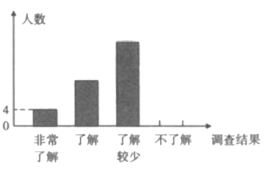
��1�����ε����ѧ������___________�ˣ����Ƹ�У![]() ��ѧ���������˽�����������__________�ˣ�
��ѧ���������˽�����������__________�ˣ�
��2��������ͳ��ͼ����������
��3�����dz��˽�����![]() ������
������![]() ��
��![]() ����������
����������![]() ��
��![]() ����Ů���������������ȡ����ȥ�μӻ���֪ʶ���������û���״ͼ���б��ķ�������ǡ�ó鵽
����Ů���������������ȡ����ȥ�μӻ���֪ʶ���������û���״ͼ���б��ķ�������ǡ�ó鵽![]() �������ĸ��ʣ�
�������ĸ��ʣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ijУΪ�˽���꼶ѧ��˯��ʱ����������������˸�У���꼶 50 ��ѧ�����õ���һ��˯��ʱ���һ���������ݣ����£�
˯��ʱ�� | ����ֵ | Ƶ�� |
|
| 3 |
| 6 | 3 |
| 7 |
|
| 8 | 25 |
| 9 | 10 |
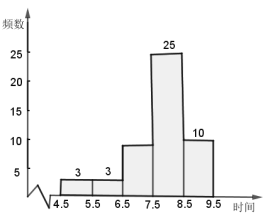
��������ͳ��ͼ������������⣺
��1��ͳ�Ʊ���![]() ��
��![]() ��
��
��2���������ݣ������У���꼶ѧ��ƽ��ÿ��˯��ʱ�䣻
��3��˯��ʱ��Ϊ 4.5~5.5h �� 3 ��ͬѧ���� 1 �������� 2 ��Ů�����ִ��������ѡ 2 ��ͬѧȥҽԺ���н�����죬������״ͼ�����б������ǡ��ѡ�С�1 �� 1 Ů���ĸ��ʣ�
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com