
【题目】解方程组:(1)![]() +
+![]() -4=0 ;(2)
-4=0 ;(2)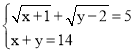
【答案】(1)![]() ,
,![]() ;(2)
;(2)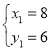 ,
, .
.
【解析】
(1)先去分母,将分式方程化为一元二次方程,然后解答即可,注意分式方程验根;
(2)先设![]() =m,
=m,![]() =n,则x=m2-1,y=n2+2,然后将方程化为一元二次方程,然后解答即可.
=n,则x=m2-1,y=n2+2,然后将方程化为一元二次方程,然后解答即可.
解:(1)去分母,得x2+(1-x)(3-3x)-4x(1-x)=0,
去括号,得x2+3-3x-3x+3x2-4x+4x2=0,
合并同类项,得8x2-10x+3=0,
分解因式,得(2x-1)(4x-3)=0,
∴2x-1=0或4x-3=0,
∴x1=![]() ,x2=
,x2=![]() ,
,
检验:将x1=![]() 代入分式方程,左边=0=右边,
代入分式方程,左边=0=右边,
将x2=![]() 代入分式方程,左边=0=右边,
代入分式方程,左边=0=右边,
因此x1=![]() ,x2=
,x2=![]() 是分式方程的根.
是分式方程的根.
所以原分式方程的根为x1=![]() ,x2=
,x2=![]() ;
;
(2)设![]() =m,
=m,![]() =n,则x=m2-1,y=n2+2,
=n,则x=m2-1,y=n2+2,
原方程组可化为
由①,得m =5-n③
③代入②,得(5-n)2+n2=13,
整理,得2n2-10n+12=0,
即n2-5n+6=0,
解这个方程,得n =2或3,
∴![]()
∴原方程组的解为![]() .
.


科目:初中数学 来源: 题型:
【题目】如图,在![]() 中,
中,![]() ,
,![]() ,点
,点![]() ,
,![]() 分别是
分别是![]() ,
,![]() 的中点,点
的中点,点![]() 为射线
为射线![]() 上一动点,连结
上一动点,连结![]() ,作
,作![]() 交射线
交射线![]() 于点
于点![]() .
.
(1)当点![]() 在线段
在线段![]() 上时,求
上时,求![]() 与
与![]() 的大小关系;
的大小关系;
(2)当![]() 等于多少时,
等于多少时,![]() 是等腰三角形.
是等腰三角形.
查看答案和解析>>
科目:初中数学 来源: 题型:
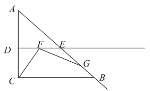
【题目】在Rt△ABC中,∠BAC=90°,过点B的直线MN∥AC,D为BC边上一点,连接AD,作DE⊥AD交MN于点E,连接AE.
(1)如图①,当∠ABC=45°时,求证:AD=DE;理由;
(2)如图②,当∠ABC=30°时,线段AD与DE有何数量关系?并请说明理由;
(3)当∠ABC=α时,请直接写出线段AD与DE的数量关系.(用含α的三角函数表示)

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,∠ABC=60°,BC=2,CD是△ABC的一条高线.若E,F分别是CD和BC上的动点,则BE+EF的最小值是_____.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在正方形![]() 中,
中,![]() 为直线
为直线![]() 上一动点(不与端点
上一动点(不与端点![]() 重合),以
重合),以![]() 为直角边在
为直角边在![]() 右侧作等腰直角三角形
右侧作等腰直角三角形![]() 连接
连接![]() .
.
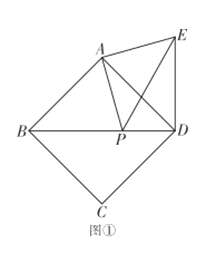
(1)如图①,当点![]() 在线段
在线段![]() 上时,线段
上时,线段![]() 和
和![]() 的数量关系为 ;
的数量关系为 ;
(2)如图②,当点![]() 在线段
在线段![]() 延长线上时,线段
延长线上时,线段![]() 和
和![]() 之间又有怎样的数量关系?写出你的猜想,并给予证明;
之间又有怎样的数量关系?写出你的猜想,并给予证明;
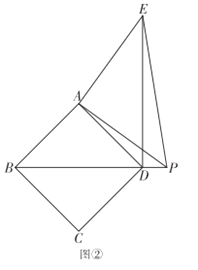
(3)如图③,当点![]() 在线段
在线段![]() 反向延长线上时,且点
反向延长线上时,且点![]() 分别在直线
分别在直线![]() 的两侧,请直接写出线段
的两侧,请直接写出线段![]() 和
和![]() 的数量关系为 ;
的数量关系为 ;

查看答案和解析>>
科目:初中数学 来源: 题型:
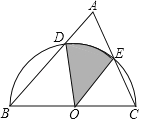
【题目】如图,在△ABC中,∠A=65°,BC=6,以BC为直径的半圆O与AB、AC分别交于点D、E,则图中由O、D、E三点所围成的扇形面积等于_____.(结果保留π)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某校组织数学兴趣探究活动,爱思考的小实同学在探究两条直线的位置关系查阅资料时发现,两条中线互相垂直的三角形称为“中垂三角形”.如图1、图2、图3中,![]() 、
、![]() 是
是![]() 的中线,
的中线,![]() 于点
于点![]() ,像
,像![]() 这样的三角形均称为“中垂三角形”.
这样的三角形均称为“中垂三角形”.
(特例探究)
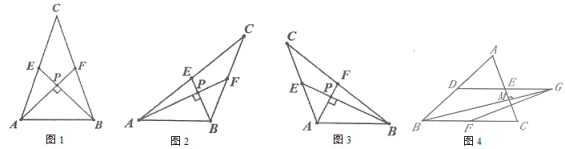
(1)如图1,当![]() ,
,![]() 时,
时,![]() _____,
_____,![]() ______;
______;
如图2,当![]() ,
,![]() 时,
时,![]() _____,
_____,![]() ______;
______;
(归纳证明)
(2)请你观察(1)中的计算结果,猜想![]() 、
、![]() 、
、![]() 三者之间的关系,用等式表示出来,并利用图3证明你的结论;
三者之间的关系,用等式表示出来,并利用图3证明你的结论;
(拓展证明)
(3)如图4,在![]() 中,
中,![]() ,
,![]() ,
,![]() 、
、![]() 、
、![]() 分别是边
分别是边![]() 、
、![]()
![]() 的中点,连结
的中点,连结![]() 并延长至
并延长至![]() ,使得
,使得![]() ,连结
,连结![]() ,当
,当![]() 于点
于点![]() 时,求
时,求![]() 的长.
的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】关于![]() 边形,甲、乙、丙三位同学有以下三种说法:
边形,甲、乙、丙三位同学有以下三种说法:
甲:五边形的内角和为![]()
乙:正六边形每个内角为![]()
丙:七边形共有对角线14条
(1)判断三种说法是否正确,并对其中你认为不对的说法用计算进行说明
(2)若![]() 边形的对角线共35条,求该
边形的对角线共35条,求该![]() 边形的内角和
边形的内角和
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com