
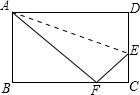
 如图,长方形ABCD沿AE折叠,使D点落在BC边上的F点处,如果∠BAF=55°,则∠AEF为多少度?
如图,长方形ABCD沿AE折叠,使D点落在BC边上的F点处,如果∠BAF=55°,则∠AEF为多少度? 解:由题意得:
解:由题意得:| 180°-∠DAF |
| 2 |


 名校课堂系列答案
名校课堂系列答案科目:初中数学 来源: 题型:
查看答案和解析>>
科目:初中数学 来源: 题型:
 如图经过原点的抛物线y=ax2+bx经过点A、B两点,其中OB=12,且
如图经过原点的抛物线y=ax2+bx经过点A、B两点,其中OB=12,且查看答案和解析>>
科目:初中数学 来源: 题型:
查看答案和解析>>
科目:初中数学 来源: 题型:
 据绝对值的几何意义,方程|x-1|+|x+2|=5表示求在数轴上与1和-2的距离之和等于5的点对应的x的值.在数轴上,1和-2的距离之和为3,所以满足方程的x的对应点在1的右边或-2的左边;若x对应点在1的右边,由图可看出x=2;同时,若x对应点在-2的左边,可得x=-3,所以原方程的解是x=2或x=-3.
据绝对值的几何意义,方程|x-1|+|x+2|=5表示求在数轴上与1和-2的距离之和等于5的点对应的x的值.在数轴上,1和-2的距离之和为3,所以满足方程的x的对应点在1的右边或-2的左边;若x对应点在1的右边,由图可看出x=2;同时,若x对应点在-2的左边,可得x=-3,所以原方程的解是x=2或x=-3.查看答案和解析>>
科目:初中数学 来源: 题型:
查看答案和解析>>
科目:初中数学 来源: 题型:
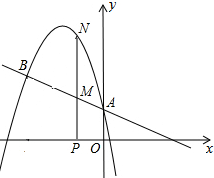 如图,二次函数y=-
如图,二次函数y=-| 5 |
| 4 |
| 1 |
| 2 |
查看答案和解析>>
科目:初中数学 来源: 题型:
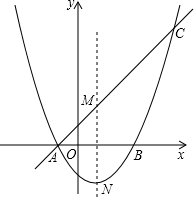 如图,抛物线y=
如图,抛物线y=| 1 |
| 2 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com